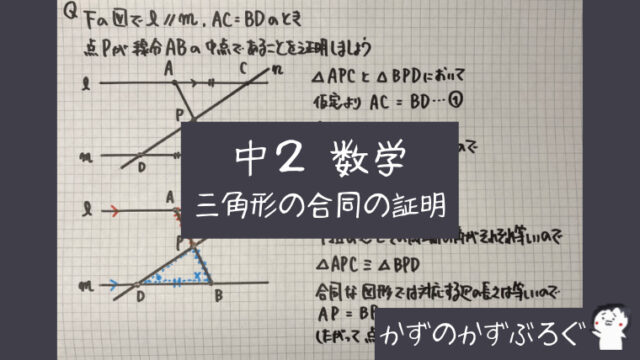
今回から
中2範囲です
まずは
「文字式の加法・減法」です
中1で
「文字式のルール」
「文字式(文字1つ)の計算」
を学習しました

この内容を使って
「文字」が
「2種類以上」の計算を
これからやっていきます
やり方は
同じなので簡単ですよ
では
一緒にやっていきましょう
単項式と多項式

まず新しい言葉を
まとめます
単項式は
「乗法だけ」となっています
「わり算は?」と思いますよね
わり算(除法)は
分数を使って表すと
「乗法」と見ることができます
【$x÷3=\frac{x}{3}=\frac{1}{3}x$】
「単項式」は
「たし算、ひき算が入っていない」と
考えましょう
項 係数 次数 ○次式

「項」「係数」については
中1で学習しましたね
もし忘れている人は
ここできちんと
確認してくださいね
ノート下の問題に
新しい言葉が
出てきます
- 多項式を「項」に分ける
- 各項の「次数」を求める
- 式の中で「一番大きい」次数を、その多項式の次数(○次式)という
定数項(数字だけの項)には
「次数」はありません
(4)の「$x^2 y$」は
$x$が「2つ」
$y$が「1つ」を合わせて
「文字が3つ」となるので
次数が「3」→「三次式」に
なります
同類項

中1では計算する
「文字の種類」は
1種類でしたね
今回は
2種類出てきます
ここで
新しい言葉です
「全く同じ」
でないといけないので
$x$と$x^2$は「違う」
と考えるので
$x$と$x^2$の項を
計算することは
できないので
注意しましょうね
多項式の計算

最後は
「多項式」と「多項式」
の計算です
「正負の数の計算」で
( )を外して計算する
方法を学習したのを
思い出してください
ノートに
あるように
多項式に()をつけて
+( )【( )の前が+】
→( )をそのまま外します
−( )【( )の前が−】
→( )の中の項の「符号」を逆にして外します
(3)(4)(5)の
ように筆算の形の問題では
「−(減法)」の時に
気をつけてください
筆算にすると
間違えてしまう人は
無理に「筆算」で計算せず
横式に直して
計算しても大丈夫です
式の加法・減法のまとめ

・単項式(たんこうしき)
数や文字の乗法だけの式のこと
・多項式(たこうしき)
単項式の和の形で表された式のこと
・次数(じすう)
単項式で、かけあわされている
「文字の数」のこと
・○次式の求め方
- 多項式を「項」に分ける
- 各項の「次数」を求める
- 式の中で「一番大きい」次数を、その多項式の次数(○次式)という
・同類項(どうるいこう)
文字の部分が
「全く同じ項」のこと
・式の( )の外し方
+( )【( )の前が+】
→( )をそのまま外します
−( )【( )の前が−】
→( )の中の項の「符号」を逆にして外します
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした