前回
新しい関数として
「$y=ax^2$」を
学習しましたね

今回は
関数と言えば
「グラフ」「変域」
「変化の割合」です
では、一緒に
見ていきましょう
$y=ax^2$のグラフ
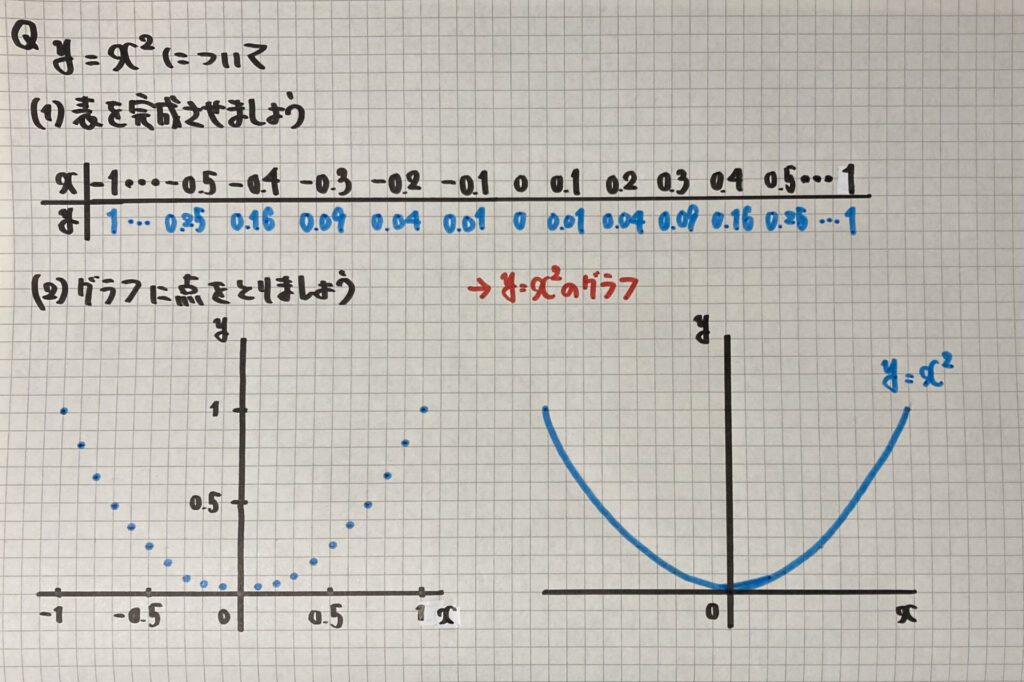
まずは
「グラフ」です
今までの
関数と同じように
- $x$と$y$の表を作る
- 座標をとる
- (直線or曲線で)結ぶ
で書いていきましょう
$y=ax^2$のグラフは
「曲線」で結んでください
「$y=ax^2$のグラフ」のまとめ
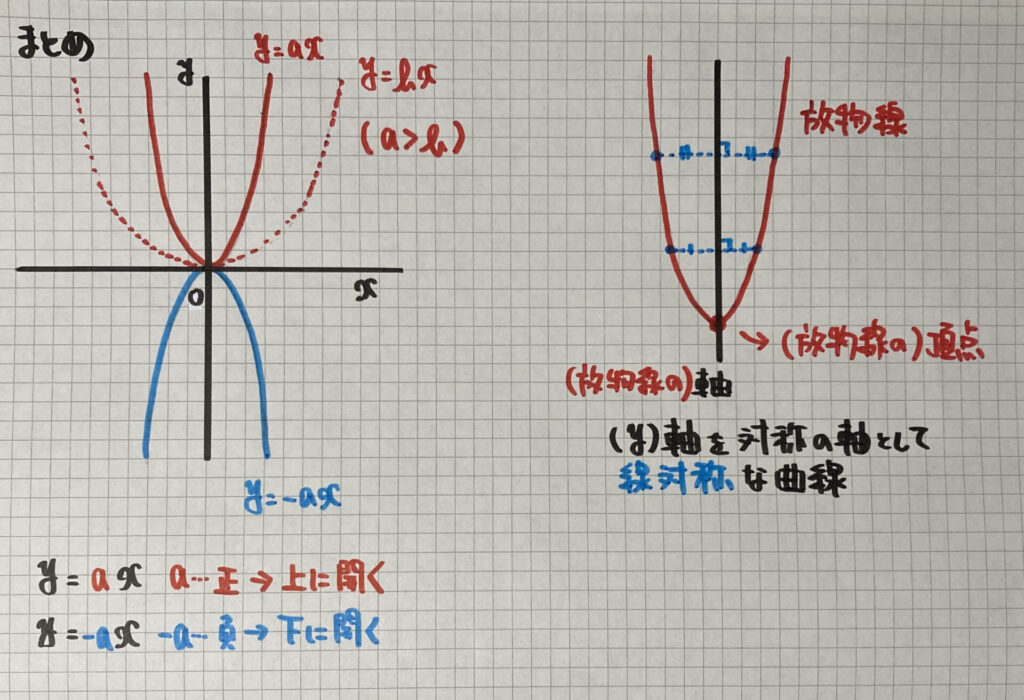
「$y=ax^2$のグラフ」の
特長をまとめましょう
変域のあるグラフ
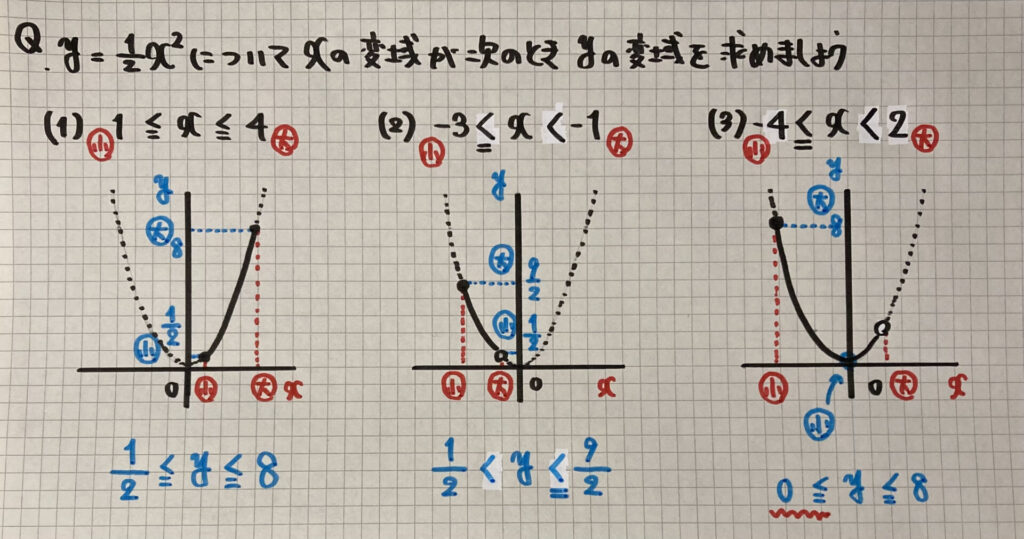
次は
「変域」です
今までに学習した
内容は大丈夫でしょうか
ポイントは
変域のあるグラフ
の書き方ですが
- 点をとる
- 原点を通る軸に対称な曲線を点線で結ぶ
- $x$($y$)の変域の点をとる※
- 変域内を実線で結ぶ
一次関数の時と
同じような注意は必要ですが
(2)は
- $x$の最小値→$y$の最大値
- $x$の最大値→$y$の最小値
と「最大」「最小」が
逆に対応していますね
(3)は
「$y=ax^2$の変域」で
よく間違える問題です
- $x$の最小値→$y$の最大値
- $x$の最大値ではなく
- 原点→$y$の最小値
変化の割合
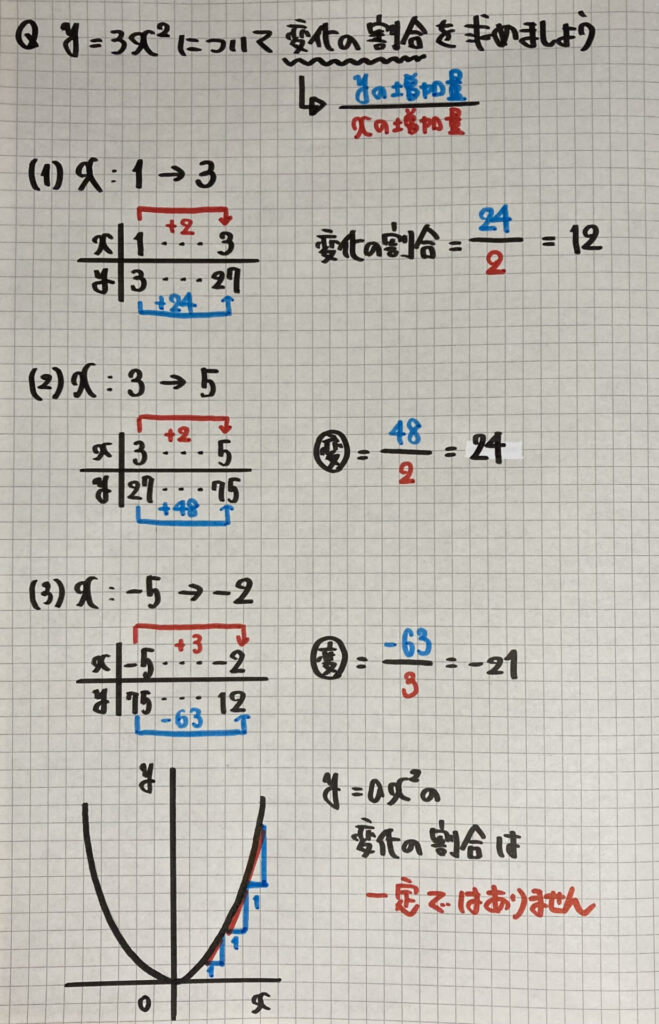
$y=ax^2$の
変化の割合は
$y=ax +b$
(一次関数)と同じく
で求めることができます
$y=ax +b$
(一次関数)の
「変化の割合=$a$」で「一定」ですが
変化の割合の公式「$a(p +q)$」
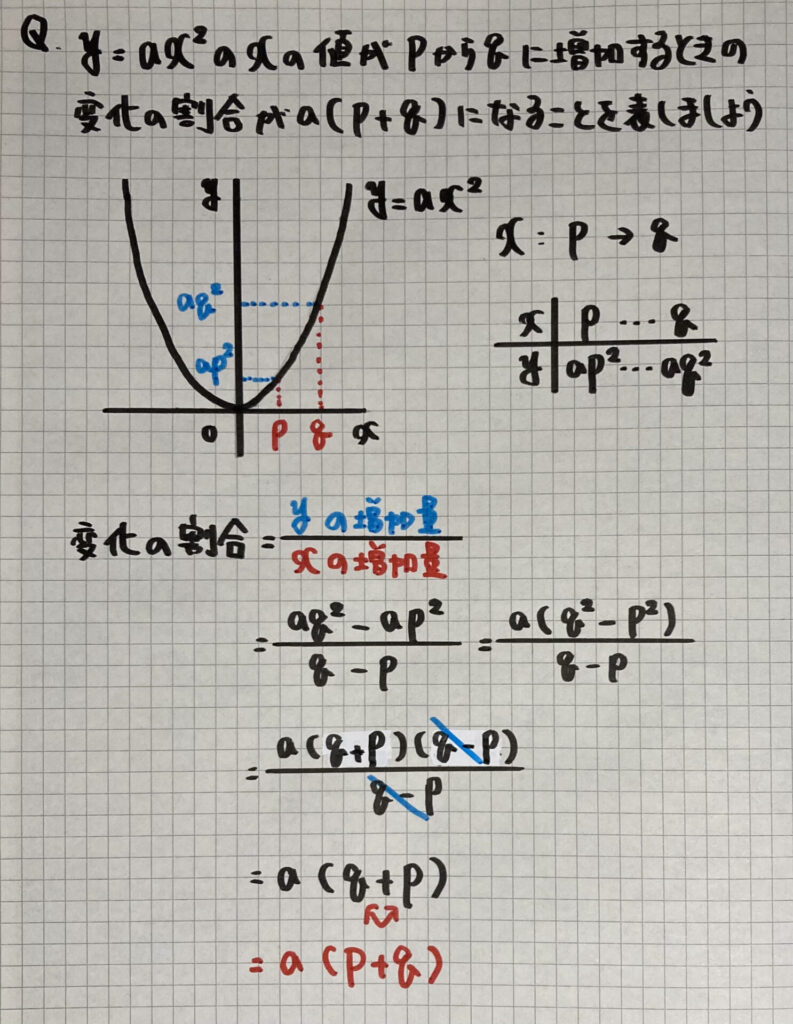
先ほど
「変化の割合」に
ついて学習しましたが
毎回
表を書いて
分数に代入して約分する
のは大変ですよね
実は
簡単に出せる
「公式」があるんです
ノートに
「公式の作り方」を
まとめました
一度、ゆっくり
確認してください
確認できれば
どんどん使って
「速く・正確」に
解きましょう
「平均の速さ」の問題

学校のテストで
よく出される問題です
まず「平均の速さ」の
意味を間違えると解くことができません
「速さの平均」と「平均の速さ」の違い
大丈夫でしようか
「速さの平均」=$\frac{速さの合計}{個数}$
となります
ここでは
「平均の速さ」の問題を
「変化の割合」の問題として考え
「公式$a(p +q)$」を
使って解きましょう
$y=ax^2$のグラフ 変域 変化の割合のまとめ

・$y=ax^2$のグラフ
「原点を通り、限りなく伸びた
曲線(放物線)で$y軸$を
『対称の軸』として線対称
- $a>0$の時→グラフは$x$軸の上にあり、上に開く
- $a<0$の時→グラフは$x$軸の下にあり、下に開く
- $a$の値が大きいほど、開き方は小さくなる
・$y=ax^2$のグラフの書き方
- $x$と$y$の表を作る
- 座標をとる
- 原点を通る曲線で結ぶ
・変域を求める問題
グラフを書いて
最小値と最大値を求める
・変域のあるグラフの書き方
- 点をとる
- 原点を通る軸に対称な曲線を点線で結ぶ
- $x$($y$)の変域の点をとる※
- 変域内を実線で結ぶ
・変化の割合
変化の割合=$\frac{yの増加量}{xの増加量}$
・変化の割合の公式
$y=ax^2$で
$xがpからqに増加した時の$
$変化の割合=a(p +q)$
・平均の速さ
=$\frac{かかった道のり}{かかった時間}$
=変化の割合
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずでした