前回
「相似な図形」
「三角形の相似条件」
について
学習しました
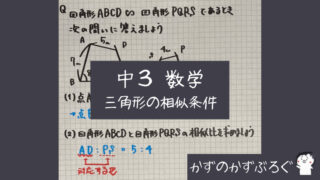
【中3数学】「相似な図形 三角形の相似条件」の問題 どこよりも簡単な解き方・求め方今回、学習するのは「相似な図形」です 「相似(そうじ)」な図形は一方の図形を拡大、または縮小したものと「他方の図形が合同である」(形は同じで大きさが違う)図形のこと 実は、「算数」で学習した「拡大図と縮図」です「数学」で新しく学習することは「記号」「相似比」「相似条件」を一緒に見ていきましょう...
今回は
中2で学習した
「合同の証明」
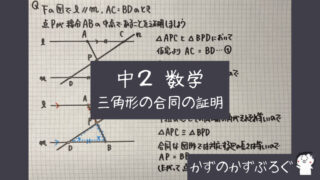
【中2数学】「三角形の合同の証明」の問題 どこよりも簡単な解き方・求め方今回は三角形の合同を使った「対応する辺の長さが等しい」「対応する角の大きさが等しい」証明を一緒に見ていきましょう...
のように
「相似の証明」
について
一緒に見ていきましょう
書き方の
大きな形は
同じなので
安心してください
「折り返し」の相似
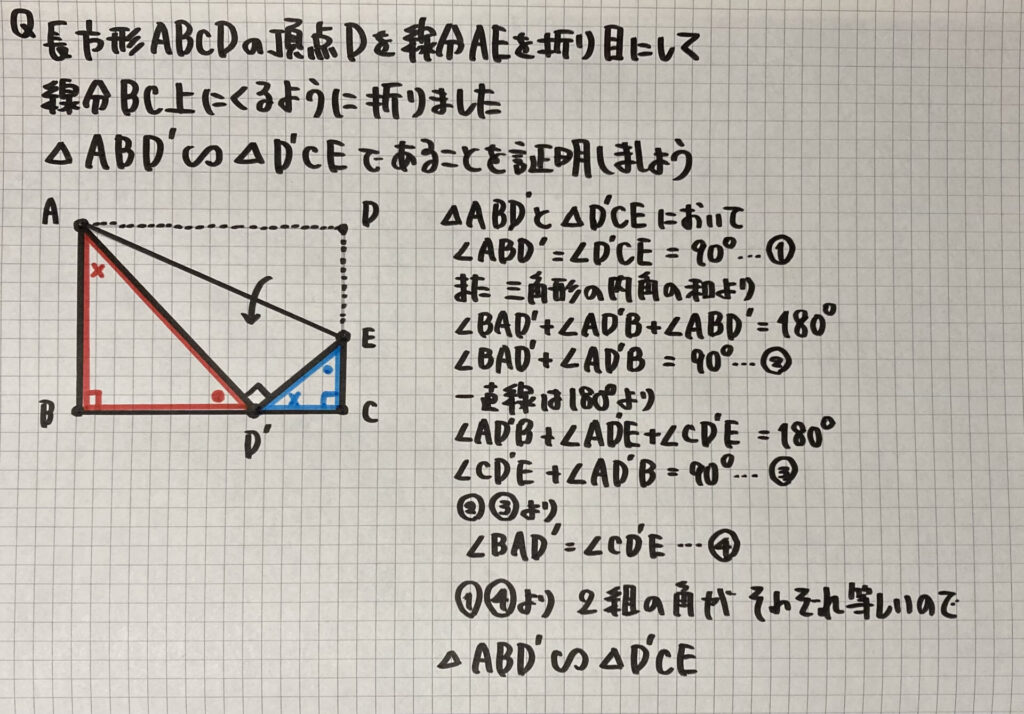
一直線に直角が刺さった形
有名な問題です
- 三角形の内角の和…180°
- 一直線…180°
を利用して
同じ角を見つけましょう
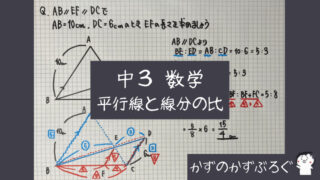
「平行」の証明
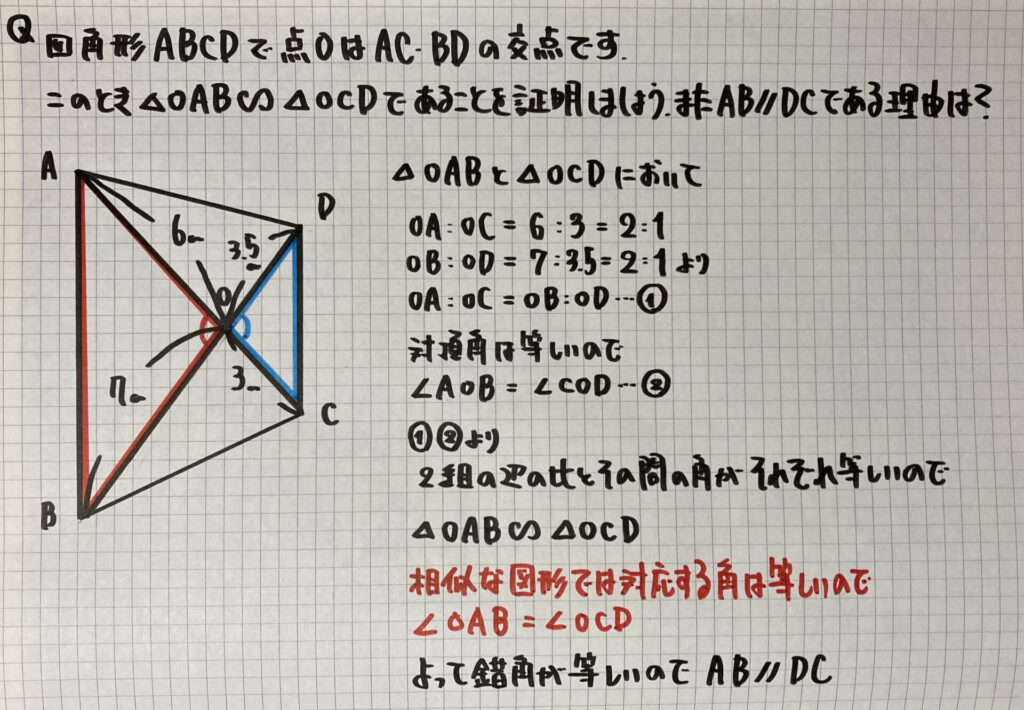
線分の長さの「比」と
間の角(対頂角)で
相似を証明しましょう
「合同」から「平行」を
証明した問題と
同じ流れの証明です
の流れで証明しています
「二等辺三角形」の相似

二等辺三角形の内部に
「二等辺三角形」がある
問題です
ことを利用しましょう
また
相似な問題では
「相似」
↓
「比例式」
↓
「線分の長さ」
を求める問題が
あります
ノートの
「△CAB∽△ADB」から
「CA:AD=AB:DB」を
作る時ですが
青と赤で
「対応している線分」に
印を入れたので
確認してくださいね
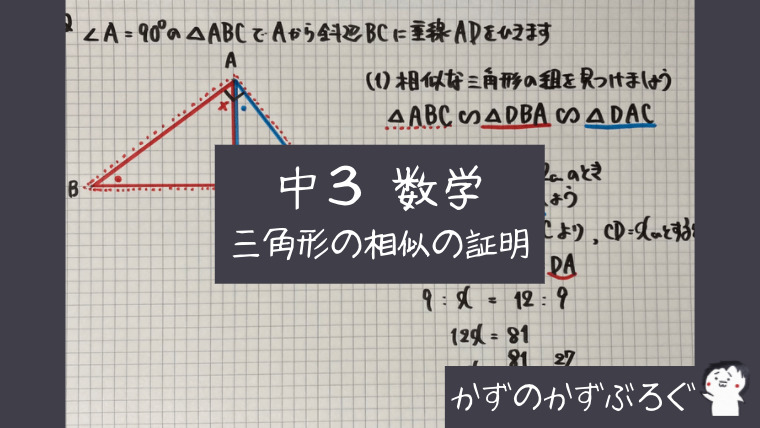
「直角三角形」の相似
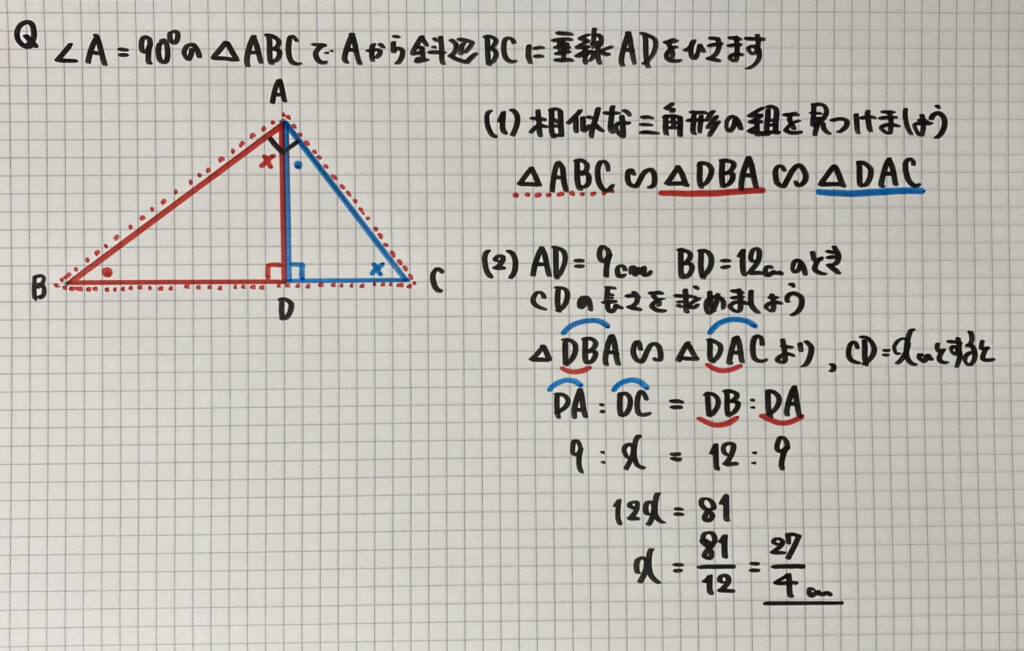
直角三角形で
頂点から斜辺に垂線を引く
有名な問題です
(1)に
あるように
相似な三角形は「3つ」
あります
直角「90°」以外の
角に「●」と「×」の
印を入れると
見つけやすいと思いますよ
三角形の相似の証明のまとめ

・長方形の折り返し
一直線に「直角」が刺さった形
- 三角形の内角の和…180°
- 一直線…180°
を利用して
同じ角を見つける
・平行の証明
「合同」と同じように
相似の証明
↓
対応する角は等しい
↓
錯角が等しいので「平行」
と証明することができる
・二等辺三角形の内部の二等辺三角形
- 共有の角
- 二等辺三角形の底角が等しい
を利用して
相似の証明ができる
・直角三角形と垂線
直角三角形の頂点から
垂線を引くと
「3つ」の
相似な三角形が
あります
かずのかず
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした