中2で
「三角形の合同」
を学習しました
【中2数学】「三角形の合同」の問題 どこよりも簡単な解き方・求め方今回は「合同な図形」について学習します 算数でも学習した内容です ここでは「三角形の種類」「三角形の合同条件」について一緒にやっていきましょう...
でしたね
今回、学習するのは
「相似な図形」です

実は、「算数」でも
学習しました
「拡大図と縮図」です
【小6算数】「拡大図と縮図」の問題 どこよりも簡単な解き方・求め方「拡大図」と「縮図」とは「形」は同じで「大きさ」が違う図形のことです 対応する「角の大きさは等しい」「辺の長さの比は等しい」文章題を解くときは「単位をそろえること」に気をつけましょう...
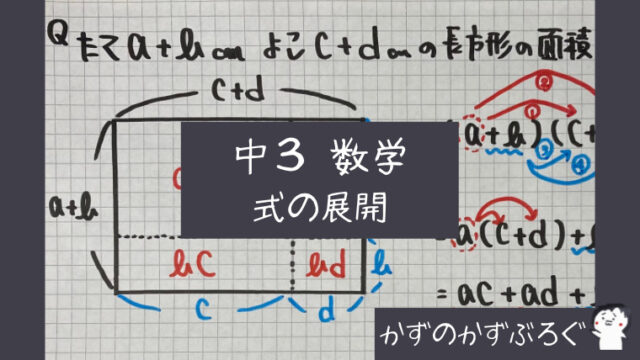
「数学」で
新しく学習することは
- 「記号$∽$」
- 「相似比」
- 「相似条件」
です
では、一緒に
見ていきましょう
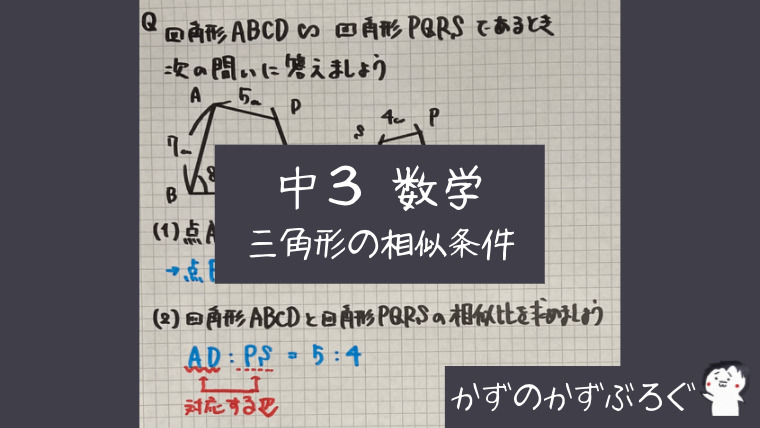
相似な図形
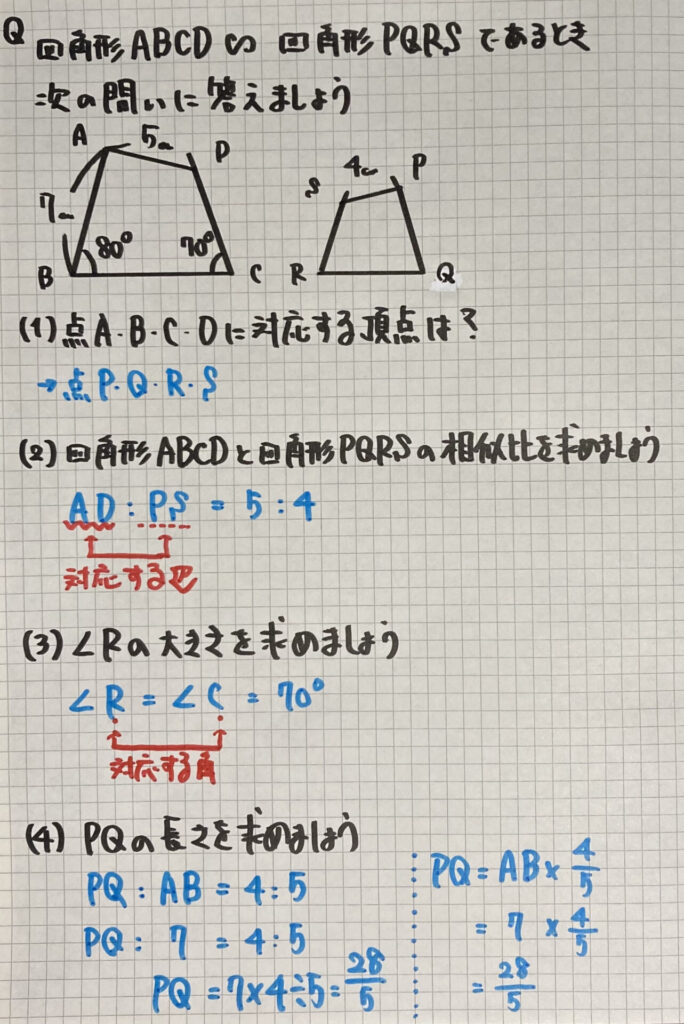
向きが違う
「相似な図形」の問題です
(4)は
対応している辺で
「比例式」を作り
長さを出すことができます
また
(右側のように)
「相似比」を
「比の値」に利用して
求めることもできます
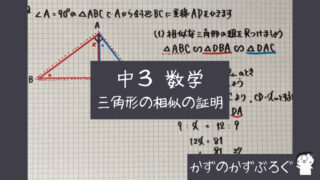
三角形の相似条件
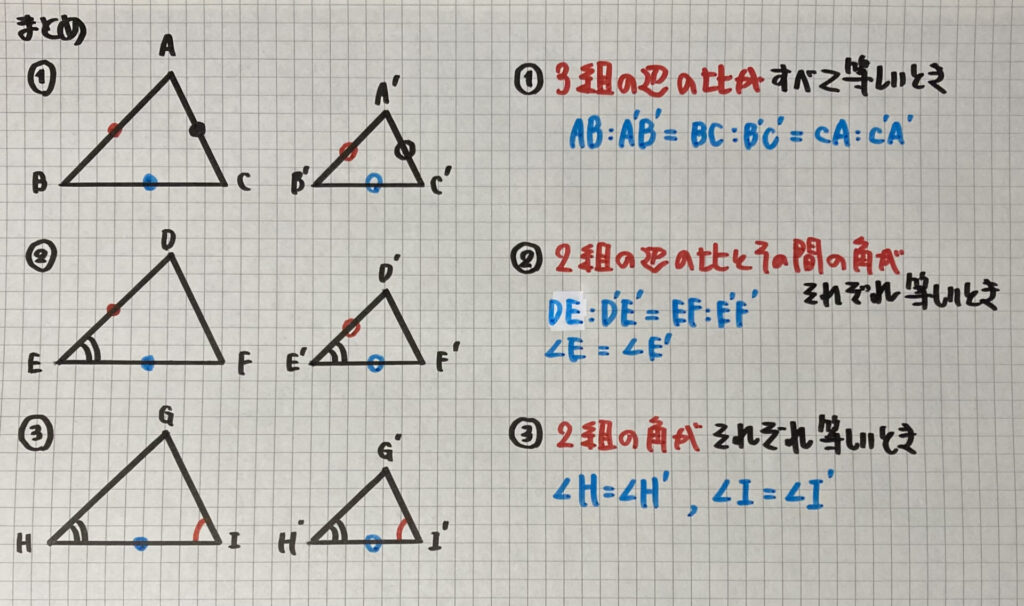
三角形の
「合同条件」は
以前、学習しましたね
相似条件も「3つ」ありますので
まとめておきますね
先生、教科書によって
「相似条件の文」に
少し違いがあることがあります
学校のテストでは
「習った文」で書けるように
しておきましょう
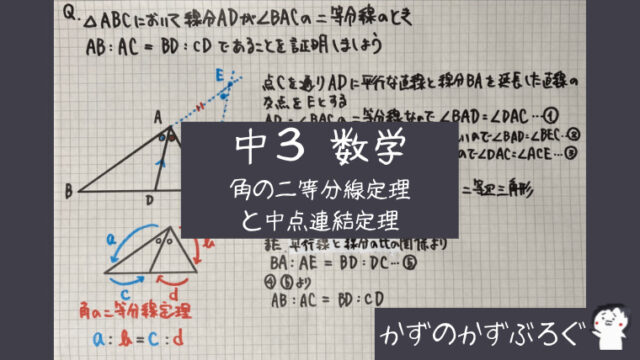
練習問題
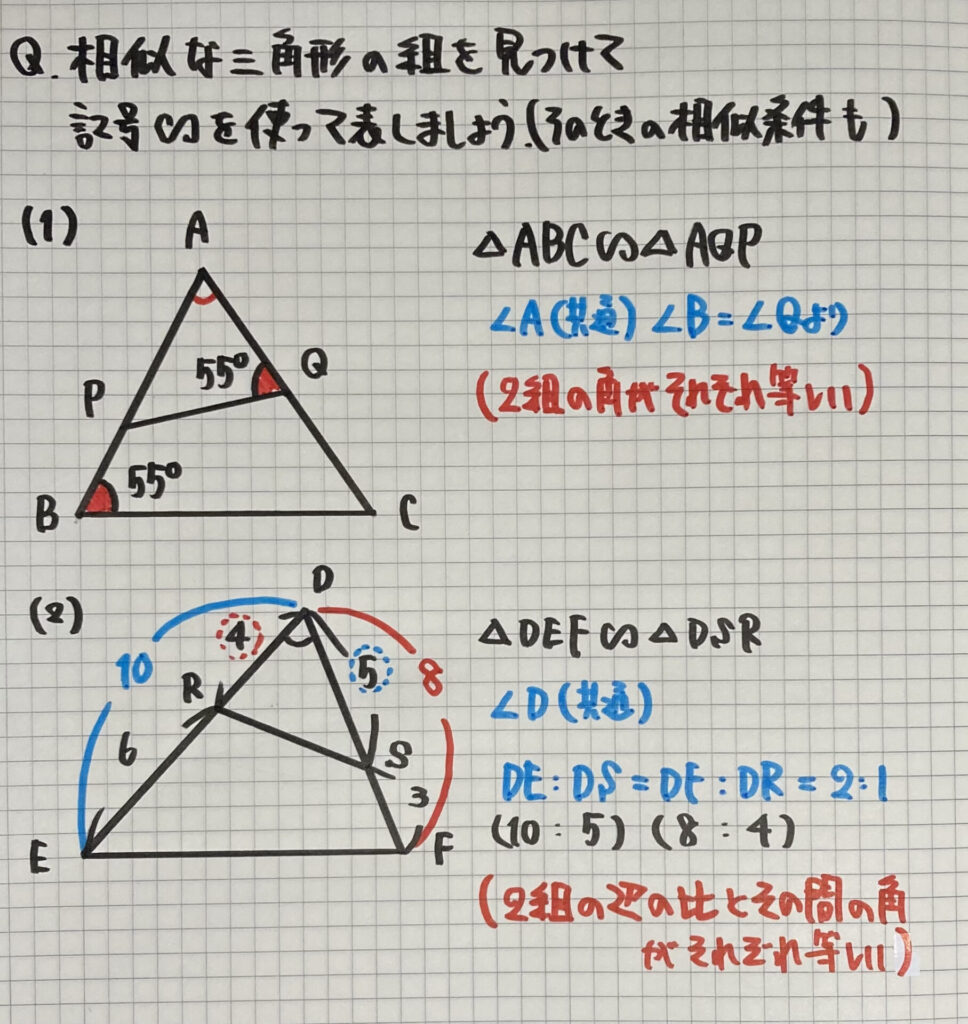
- $\angle A$(共通)
- $\angle A$(共通)
のような
1つの角を共有する
「相似」がよく出てきます
相似な図形 三角形の相似条件のまとめ

・「相似(そうじ)」な図形は
一方の図形を
- 拡大、または
- 縮小したものと
「他方の図形が合同である」
(形は同じで大きさが違う)
図形のこと
・相似の表し方
四角形ABCD$∽$四角形EFGH
「∽(相似)」と読みます
・相似比
相似な2つの図形で、対応する線分の長さの比のこと
・相似な図形の性質
- 対応する線分の長さの「比」は、全て等しい
- 対応する角の大きさは、それぞれ等しい
・三角形の相似条件
- 3組の辺の比が、すべて等しい
- 2組の辺の比とその間の角が、それぞれ等しい
- 2組の角が、それぞれ等しい
・1角共有の相似
- 2組の角がそれぞれ等しい
- 2組の辺の比とその間の角が、それぞれ等しい
のどちらかになる
かずのかず
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずでした