今回は
「合同な図形」について
学習します
算数でも
学習した内容です
かずのかず
こちらで
確認してくださいね
【小5算数】「合同な図形」の問題 どこよりも簡単な解き方・求め方2つの図形の形と大きさが全く同じとき「2つの図形は合同である」と言います 合同な図形の対応する辺、角は等しいです 合同な三角形の書き方は中学校の数学でも大切な考え方になるので、しっかり確認しておきましょう
...
ここでは
「三角形の合同」
についてです
では、一緒に
やっていきましょう
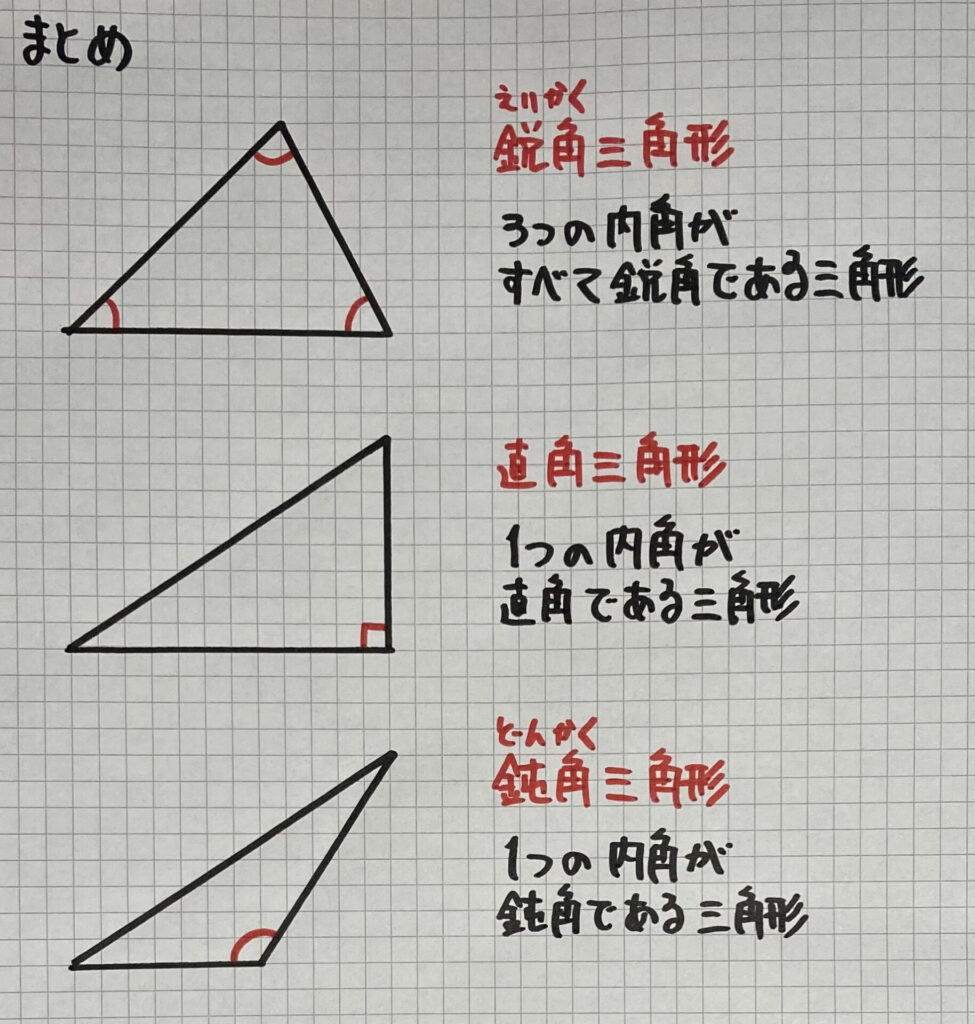
三角形の種類
合同な図形の前に
「三角形の種類」
についてです
ノートにありますが
ここでも
まとめておきます
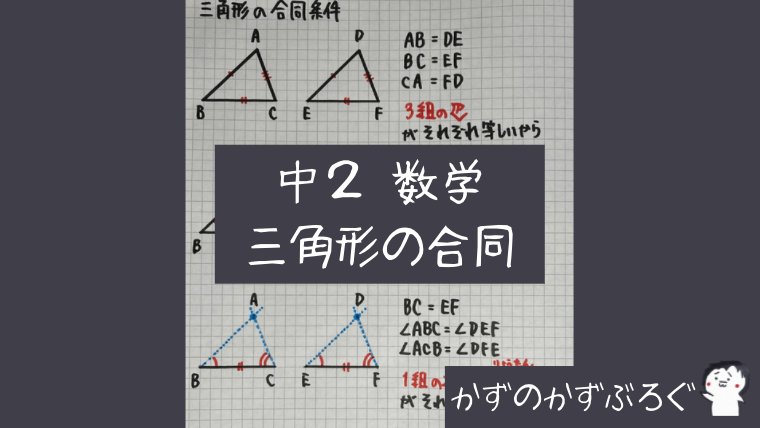
三角形の合同条件
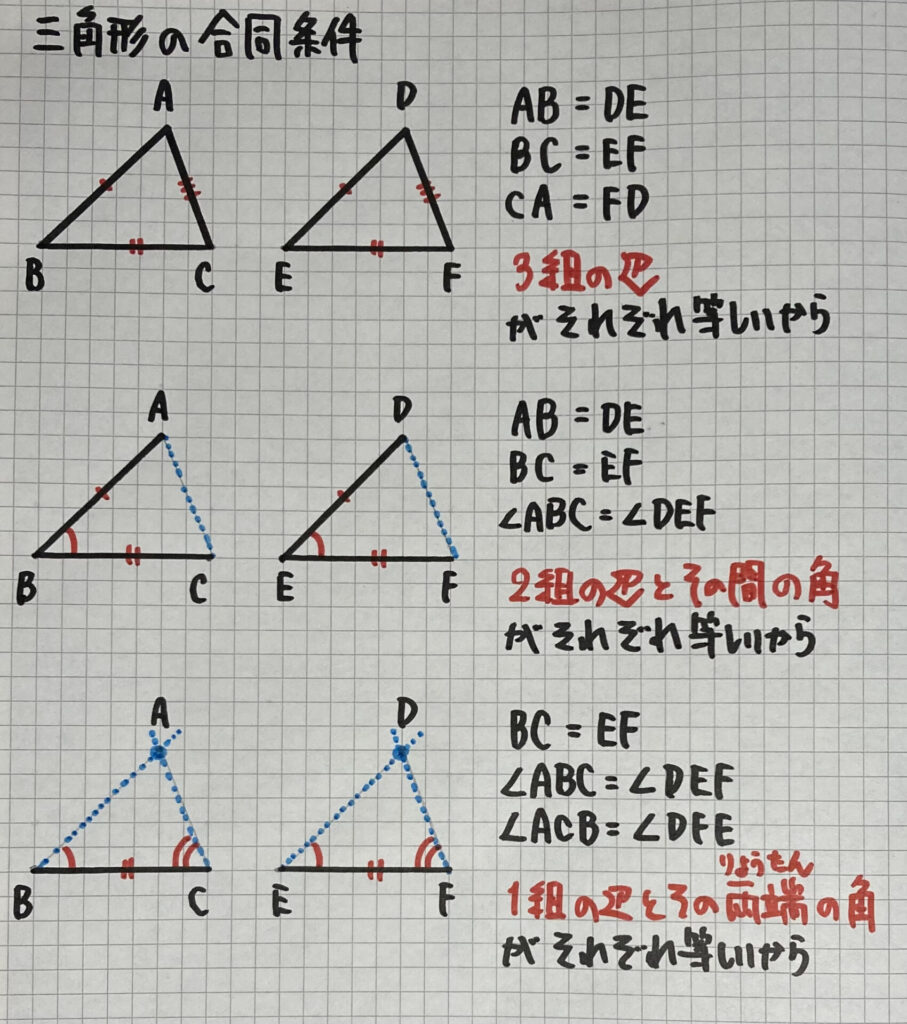
算数で学習した
「合同な三角形の書き方」
と同じ内容です
もし、忘れていても
大丈夫です
今回でしっかり
覚えましょうね
先生、教科書によって
「合同条件の文」に
少し違いがあることがあります
学校のテストでは
「習った文」で書けるように
しておきましょう
練習問題①
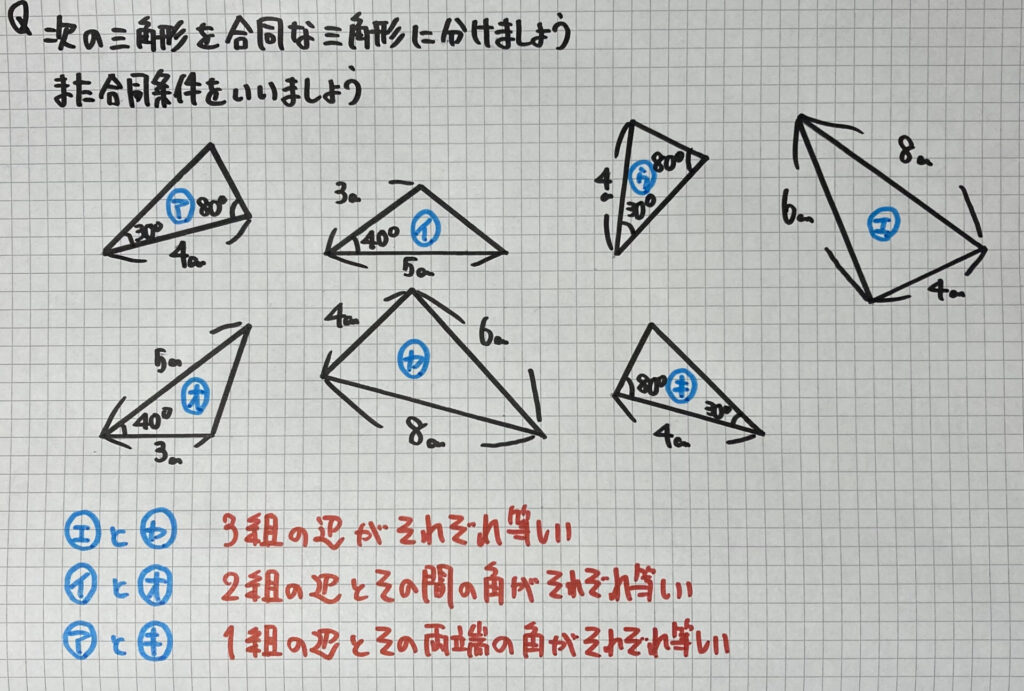
「三角形の合同条件」を
きちんと覚えていないと
解けない問題です
最初は
「合同条件」を見ながら
練習してみましょう
繰り返し解いている
うちに覚えられる
ようになりましょうね
練習問題②
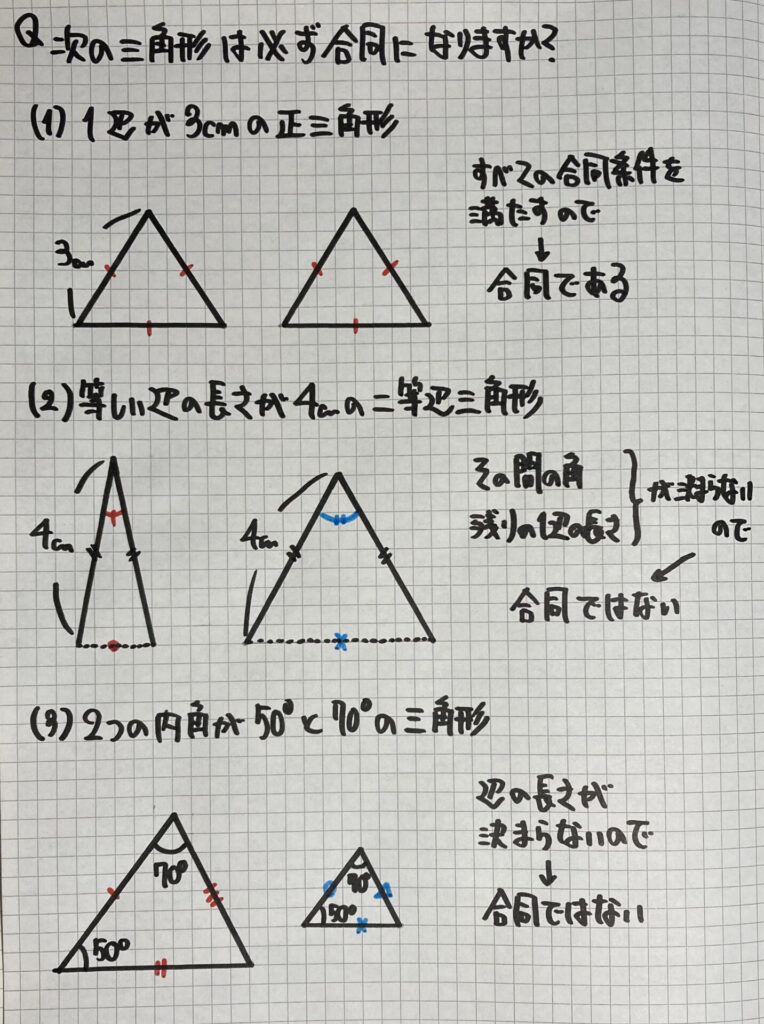
この問題は
自分で
「図形を書いて」
確認することが
必要です
「合同でない」ものが1つでもあれば
「合同である」とは言えません
2組の辺とその間にない角
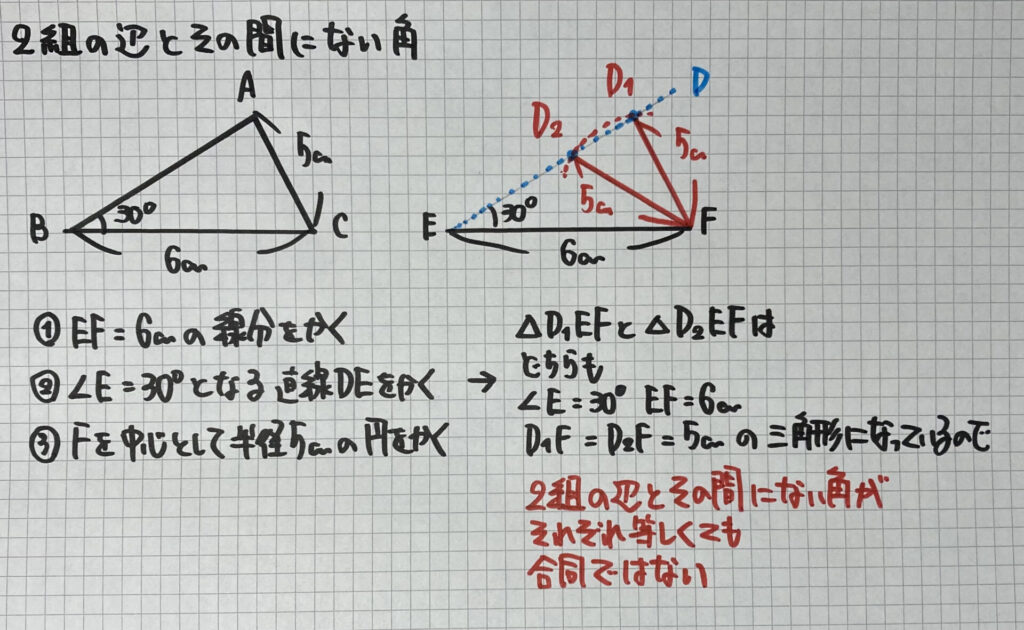
「合同条件」の
2組の辺と「その間の角」がそれぞれ等しいから
によく似た表現で
2組の辺と「その間にない角」がそれぞれ等しい場合
を見てみましょう
ノートにあるように
この条件では
DF=5cmの三角形を
2つ書くことができます
したがって
三角形の合同のまとめ

・三角形の種類
鋭角三角形
3つの内角がすべて鋭角である三角形
直角三角形
1つの内角が直角である三角形
鈍角三角形
1つの内角が鈍角である三角形
・合同の表し方
△ABC≡△DEF
「≡(合同)」と読みます
・三角形の合同条件
- 3組の辺が、それぞれ等しい
- 2組の辺とその間の角が、それぞれ等しい
- 1組の辺とその両端の角が、それぞれ等しい
・合同な図形の性質
対応する
- 線分の長さ
- 角の大きさ
はそれぞれ等しくなります
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした