前回、新しい考え方
「正負の数」をやりました
ここでは
「正負の数の加法と減法」を
やっていきましょう
数直線を使って

まずは
「数直線」を使う方法です
( )の中の
「+」を「プラス」
「−」を「マイナス」と読んで
( )の外の
「+」を「たす」
「−」を「ひく」と読みましょう
(+3)+(−2)は
「(プラス3)たす(マイナス2)」
と読みます
前の( )を<スタート地点>
+を<すすむ>
−を<もどる>
後の( )を<目もり>
として考えましょう
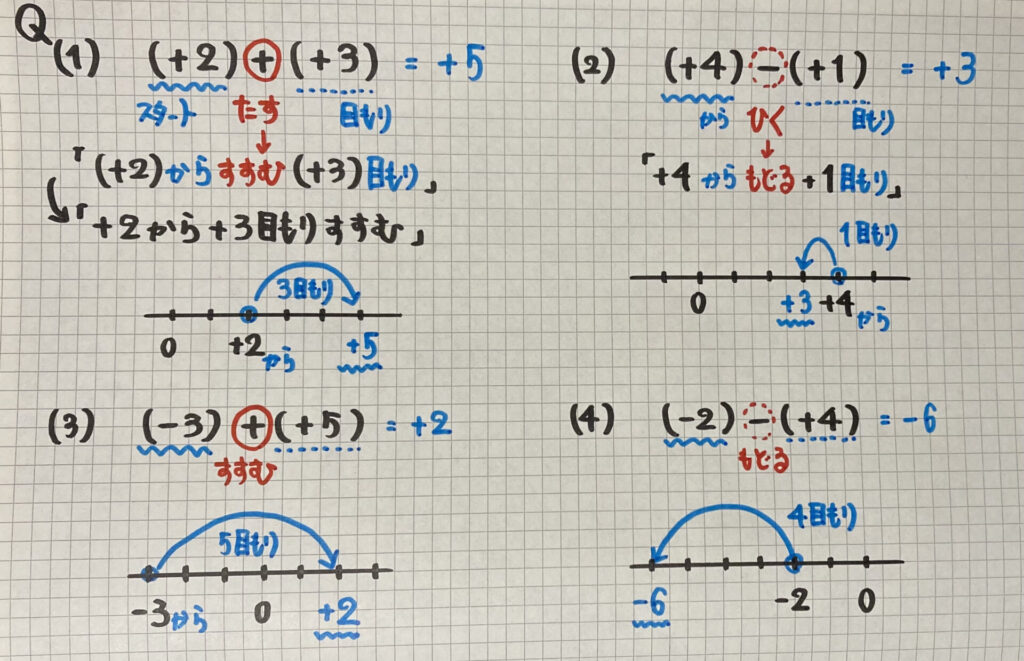
「式」を
「文」にして
「数直線」でどうなるか
で答えを求めています

後の( )<目もり>が
「負の数」のとき
「日本語」が少しおかしくなります
「…(−2)すすむ」は
少しおかしいですよね
(−2)を(+2)で反対に
<すすむ>を<もどる>で反対にして
同じ意味の文を作っています
「反対の言葉」で表す方法は
こちらで確認してくださいね
たし算 ひき算

次の考え方は
(+2)は「+」が「2つ」ある
(−3)は「−」が「3つ」ある
と考えて「たし算」「ひき算」で考えます
⑷は「ひき算」で(−)があるときは
「反対の言葉」で「たし算」にします
⑸は「たし算」で( )の符号が違う時は
「たす」を<消す>として考えます
(+)と(−)がお互いに
「消し合う」と考えます
正負の数の加法
ここまで
「数直線を使う」
「たし算ひき算」
でみてきました
「正負の数」での
「たし算」「ひき算」も
答えを出すことはできますね
『もう少し簡単な方法はないのかな…?』
『ありますよ!』
せっかく数学になったので
こんな考え方はどうでしょう
まず「言葉の意味」からです
正負の数の減法

「正負の数」の「減法」は
「反対の言葉」の考え方を使って
「加法」にして
先ほどまとめた
「加法のルール」を使います
( )の外し方「+」の省略

次は( )を外して
計算する方法です
2+3を(+2)+(+3)と
書くのは大変ですよね
項(こう)に分ける

( )を外した「数」の
1つ1つを「項」と言います
「3数以上の計算」では
- 「加法」だけの式を作って
- ( )を外す
- 「+の項」と「−の項」に分けて計算
- 「+」と「−」の数を計算します
小数と分数の計算
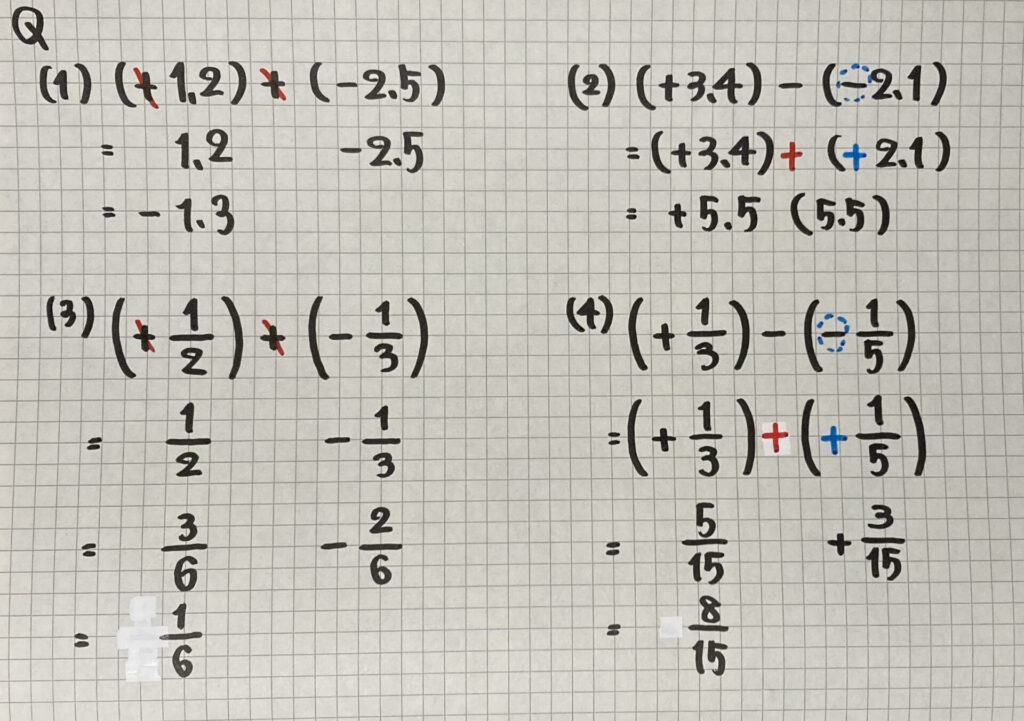
「小数」や「分数」も
「整数」と同じように
計算することができますよ
正負の数の加法 減法のまとめ

・加法…「たし算」のこと
・減法…「ひき算」のこと
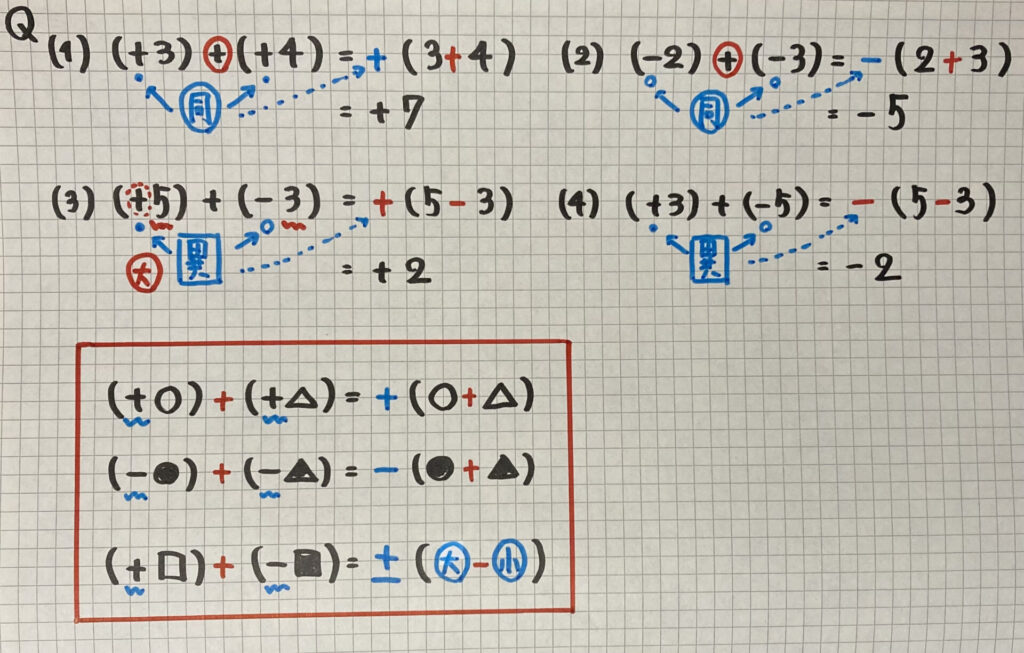
・正負の数の加法のルール
( )が同符号の時
答えの
- 「符号」は同じになる
- 「数」は「絶対値」をたしたもの です
( )が異符号の時
答えの
- 「符号」は「絶対値」が大きい方になる
- 「数」は「絶対値」をひいたもの です
・正負の数の減法は加法にして計算する
・( )の外し方
- 式の先頭の「+」
- ( )の外の「+」を消して
( )の中の「数」を外に出すイメージです
あとは「+」と「−」の数を計算しましょう
・「3数以上の計算」では
- 「加法」だけの式を作って
- ( )を外す
- 「+の項」と「−の項」に分けて計算
- 「+」と「−」の数を計算します
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした