この前、「方程式」の計算を
勉強しました
方程式の計算については

こちらで確認してくださいね
ここでは、方程式の文章題①として
「年齢」「代金」「整数」「過不足」の
問題を一緒にみていきましょう
「年齢」の問題

求めたいものが
「何」年後なので
$x$年後として
Aさんの年齢を(31+$x$)歳
Bさんの年齢を(12+$x$)歳
と表し方程式を作って
問題を解いていきます
式の2段目
31+$x$=24+$2x$
のままでも計算できますが
$−x$となるので
左辺と右辺を入れかえて
24+$2x$=31+$x$
としています
次に
ノートの右側を見てください
「方程式の文章題」の
答え方にはルールがあります
- 求めたいものを$x$として「〜を$x$とすると…と表せる」と書く
- 方程式を立てる(作る)
- 方程式を解く
- 解を求める
- 解から問題の答えを求める
「代金 個数」の問題

⑴も解き方①〜⑤の順番に
書いていきました
⑤では
方程式の解$x=7$から
ペンの本数「3本」を
10−$x$=10−7=3と
計算して求めています
「整数」の問題

⑴は
「同じ数になります」という文から
等式(方程式)を作ります
⑵は
よく出される問題です
文字($x$等)を使って整数を
表すときに注意が必要です
例えば
「十の位が3、一の位が6」の整数は「36」
ですが
「十の位が3、一の位が$x$」の整数は「$3x$」では
ありませんね
$3x$=3×$x$の意味になってしまいます
「36=10×3+1×6」と考えます
文字の時も
として考えましょう
「過不足」の問題
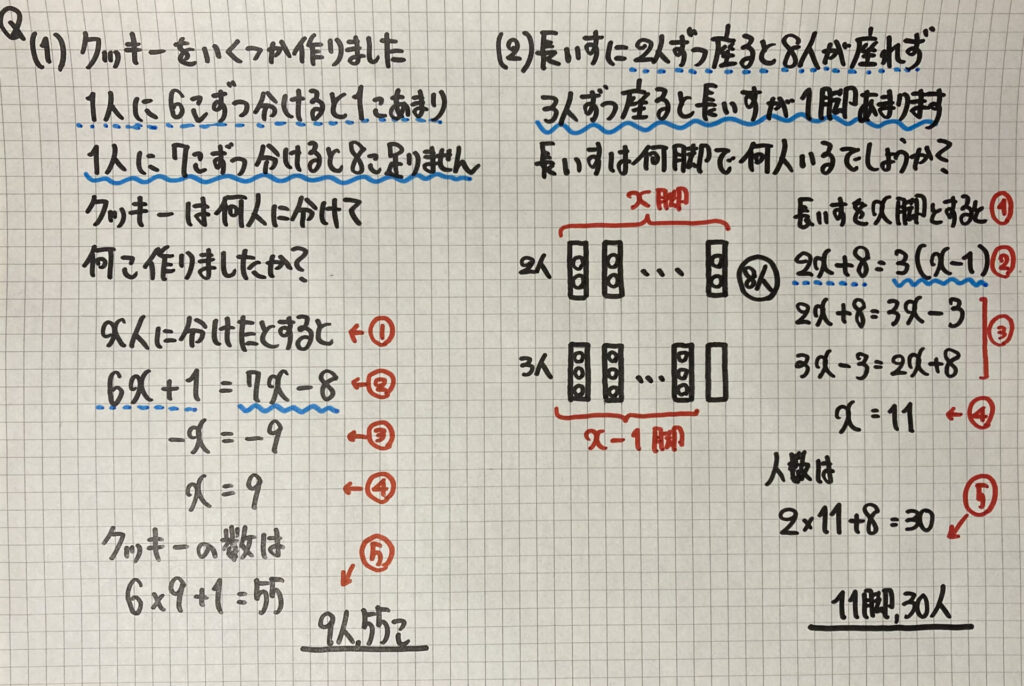
⑴では
「分けた人数」と
「クッキーの個数」の2つを求める問題です
ノートでは
「分けた人数」を「$x$人」としていますが
「クッキーの個数」を「$x$こ」として
式を作ることもできます
その時の式は
$\frac{x−1}{6}$=$\frac{x+8}{7}$
となります
少しこの考え方はややこしくなるので
おすすめは
「分けた人数」を「$x$人」の方です
そして
…分けると「1こあまる」ので「+1」
…分けると「8こ足りない」ので「−1」
のイメージで式を作ってみてくださいね
⑵では
図を書いて考えましょう
長いすを「$x$脚」として表すと
「3人」で座るときは
「$x$−1脚」と表すことができます
「⑤解から答えを求める」ときですが
「3人」で座った式、3($x$−1)に
$x=11$を代入して
答えを出すこともできます
方程式の文章題①(年齢 代金 整数 過不足)のまとめ

・方程式の文章題の解き方
- 求めたいものを$x$として「〜を$x$とすると…と表せる」と書く
- 方程式を立てる(作る)
- 方程式を解く
- 解を求める
- 解から問題の答えを求める
「解き方を書きなさい」とあれば
①〜⑤をきちんと書かないといけません
・整数の表し方
「十の位を$x$一の位を$y$」の整数は
「$xy$」ではなく「$10x$+$y$」です
・方程式の計算のコツ
方程式を解くときに
$x$の係数が「−」になるときは
左辺と右辺を入れかえて計算すると
計算ミスが減ります
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした