今回は
「多角形の角」を
学習します
基本的なところは
算数で
学習しましたので
参考にしてください
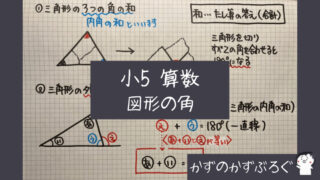
練習問題

ノートの右に
まとめましたが
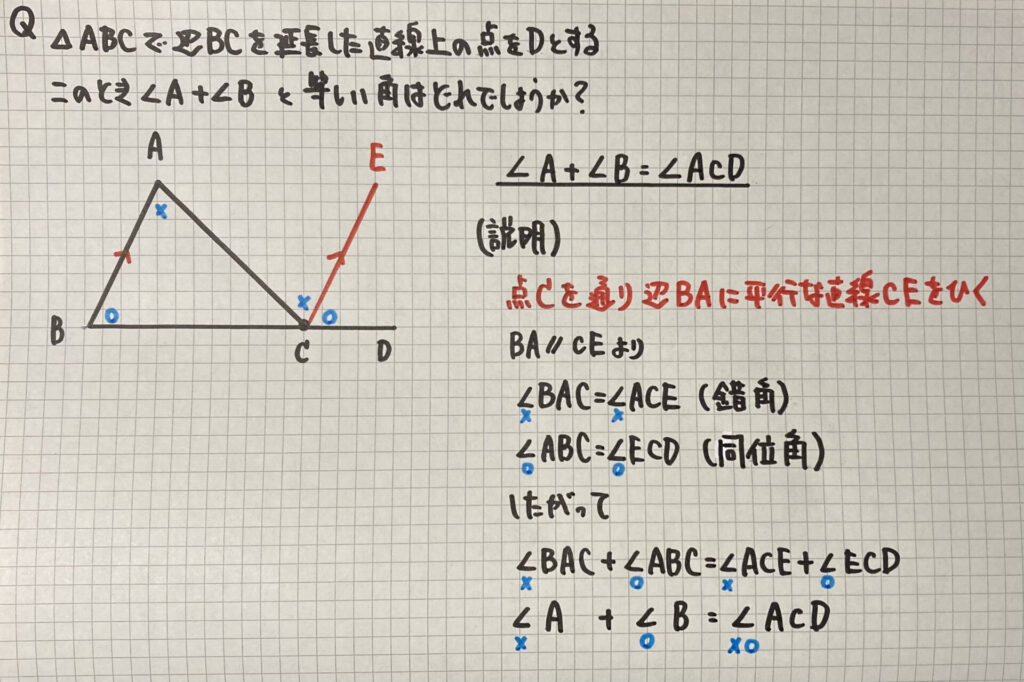
- 三角形の内角の和は180°
- 内角+外角=180°
- 三角形の外角はそれと、となり合わない2つの内角の和に等しい
の3点をしっかり
確認しておいてくださいね
多角形の内角 外角の和
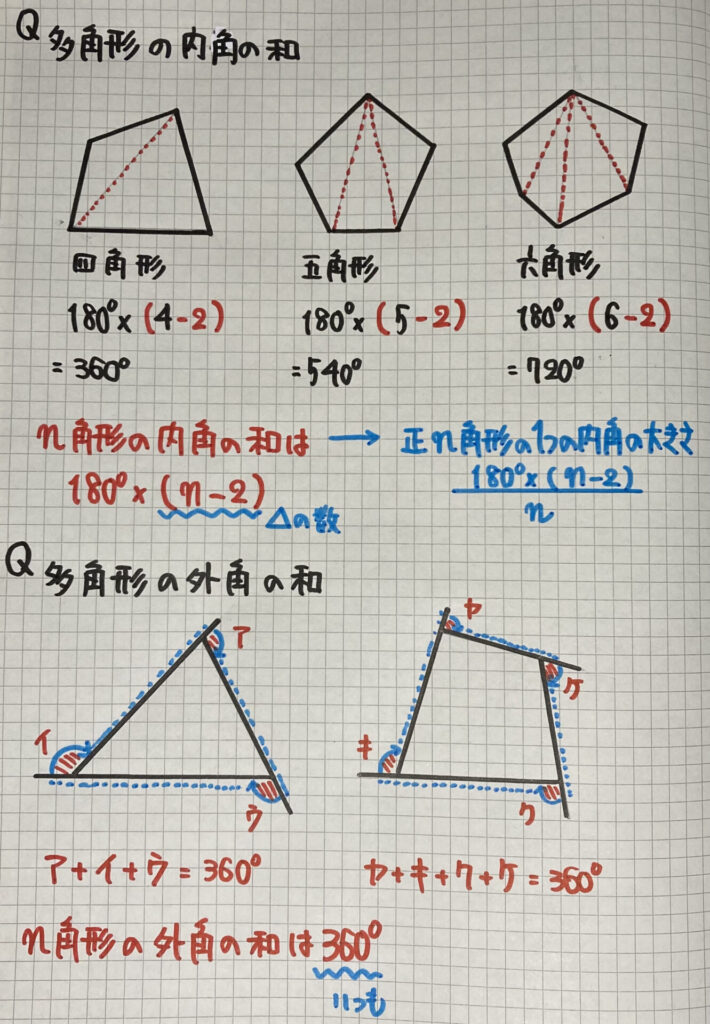
「内角の和」
については
算数でも学習しましたね
多角形を
「三角形」に分けて
考えましょう
となりますね
これを$n$で割ったものが
と表すことができます
次に
多角形の「外角の和」です
ノートの下に
あるように
どのような図形でも
360°(一定)です
練習問題

(1)は
180°×($n−2$)=1080°
という
方程式を立てて
解くことができます
(2)①は
$n$角形の外角の和は360°
を使いましょう
(3)は
内角と外角の
大きさの比が
「3:2」より
「文字$a$」を
使って
「$3a$と$2a$」
と表します
そこから外角を求めましょう
へこみのある図形
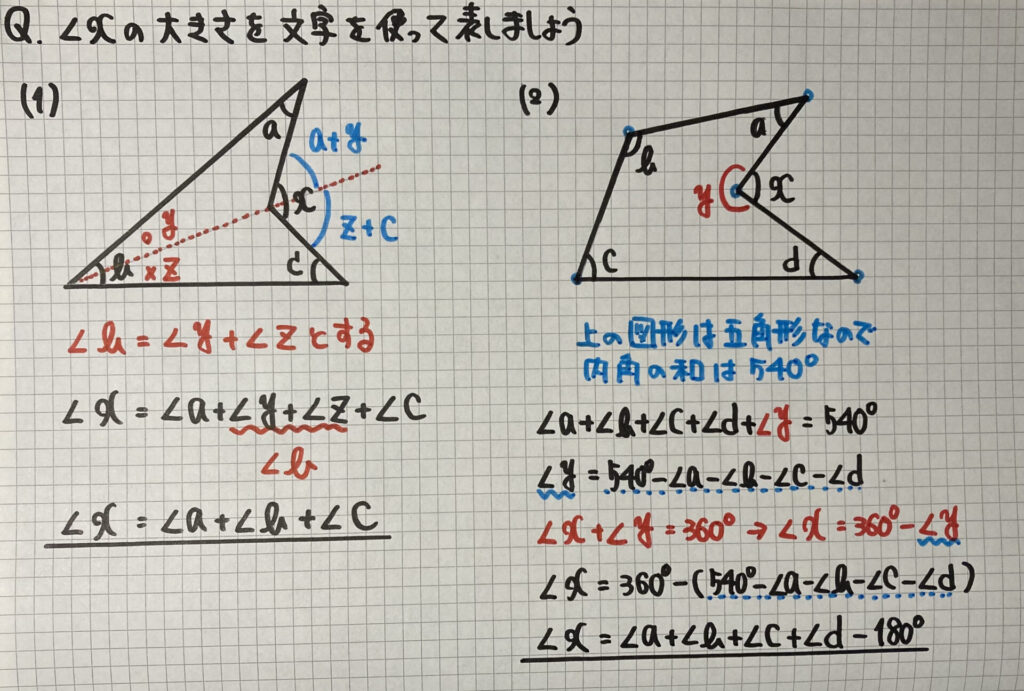
(1)は
$\angle b$と$\angle x$の
頂点を結んで
直線をひき
図形を
「2つの三角形」に
そして
「$\angle b$」を「$\angle y$と$\angle z$」に
分けましょう
外角の性質を使うと
となります
とても有名な形なので
覚えておきましょう
(2)は
この図形を「五角形」と見て
$\angle x$の
内角を$\angle y$として
「方程式」を作りましょう
少し複雑で長い式に
なるので
覚える必要はありませんので
安心してください
「式の作り方」だけ
確認しておきましょう
多角形の角のまとめ

・三角形の角の性質
- 三角形の内角の和は180°
- 内角+外角=180°
- 三角形の外角はそれと、となり合わない2つの内角の和に等しい
・$n$角形の内角の和
180°×($n−2$)
・正$n$角形の1つの内角
$\frac{180°×(n−2)}{n}$
・$n$角形の外角の和
どの多角形も「360°」
・キツネ型の四角形の角度
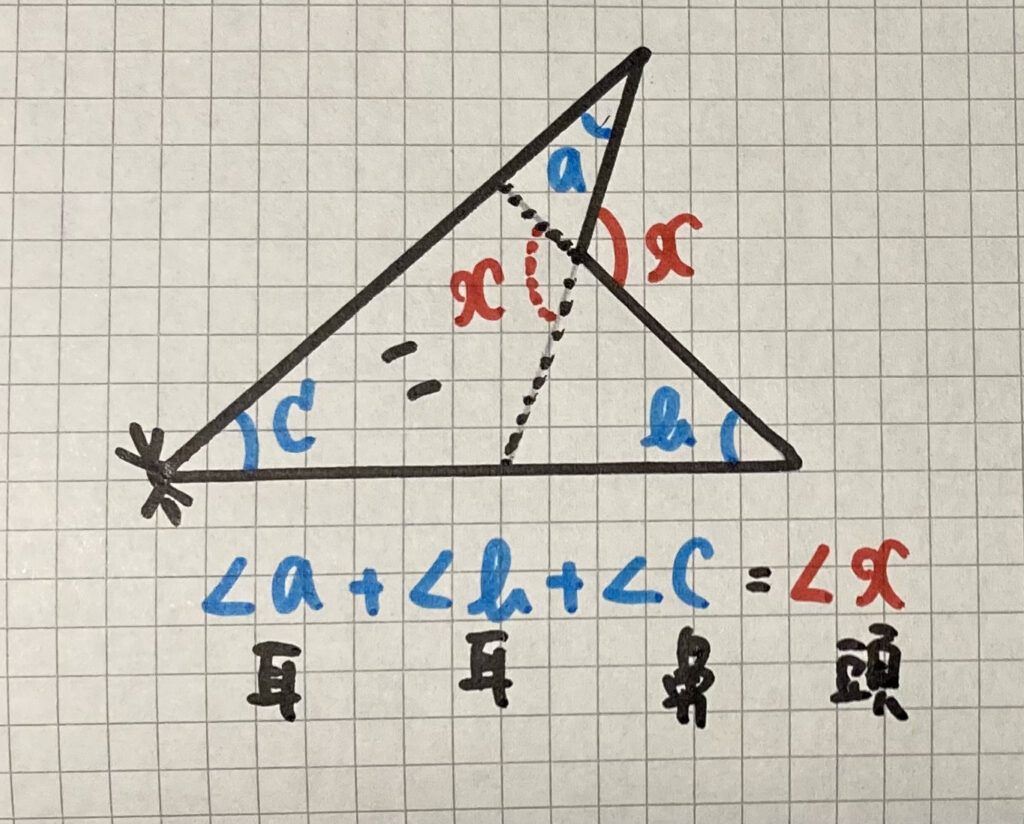
$\angle a +\angle b +\angle c=\angle x$
(耳+耳+鼻=頭)
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした