今まで算数の問題で
「分からないもの」が出てきたときに
「□(しかく)」を使った式で表すこと
があったと思います
これからは
この「□(しかく)」を
「X(エックス)」と「Y(ワイ)」の
「文字」で表していきます
中学校での「数学」では
この「文字」を使った式を
使うことが多くなります
では、実際の問題を見ていきましょう
文字の書き方

「$x$(エックス)」と「$y$(ワイ)」の
書き方を上のノートにまとめました
少し特別な書き方なので
しっかり確認しておいてくださいね
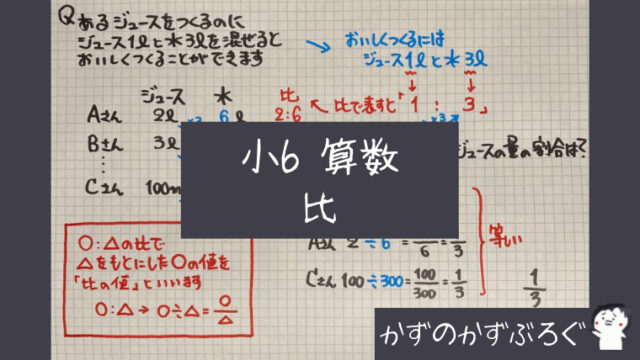
数(量)の大きさを式で表す

⑴では□の代わりに$x$を使っているだけなので
難しく考えないようにしてくださいね
⑵では□の式に「数」を入れたように
$x$に「3」をあてはめただけです
この考え方を
「代入(だいにゅう)」と言います
数(量)の関係を式で表す

「円周=直径×3.14」でしたね
直径は半径の2倍なので
「直径=半径×2」と表すことができます
それらをまとめると
「円周=半径×2×3.14」という式を
作ることができます
⑶の最後は
□が入った式の「逆算」の考え方です
例です
6=□×3
だとすると
□=6 ÷3
で求めることができますよね
□が$x$に代わっただけなので
難しく感じたら
□の式を思い出しましょうね
練習問題

「$x$(エックス)」と「$y$(ワイ)」を
「数字」と同じように「式」で使っています
上のような問題は
「文章」から
「言葉」で「式」を作って
「数字」と「文字」を当てはめてみましょう
分からない数(量)を文字で表す

⑴では、少し難しい「逆算」を使っています
左の「数字」だけの式を見比べて
確認してみてください
- 図形の面積の公式
- 速さを求める式
は大丈夫ですか
「図形の面積の公式」については
「速さ」については

こちらで確認してみてくださいね
文字と式のまとめ

・今まで分からない数(量)を
「□(しかく)」で表していたものを
「$x$(エックス)」と「$y$(ワイ)」の
「文字」で表します
・「$x$(エックス)」と「$y$(ワイ)」の書き方

・式で表した中の「文字$x$や$y$」に
「数」を当てはめることができる
以上、「算数嫌いな人が、
算数を楽しく好きになって欲しい」
かずのかずぶろぐでした