今回は
「円とおうぎ形の性質」
についてです
「算数」でも
学習しましたね
ここでは、
「数学」になってから
学習した「作図」を
使った問題も出てきますので
一緒に見ていきましょう
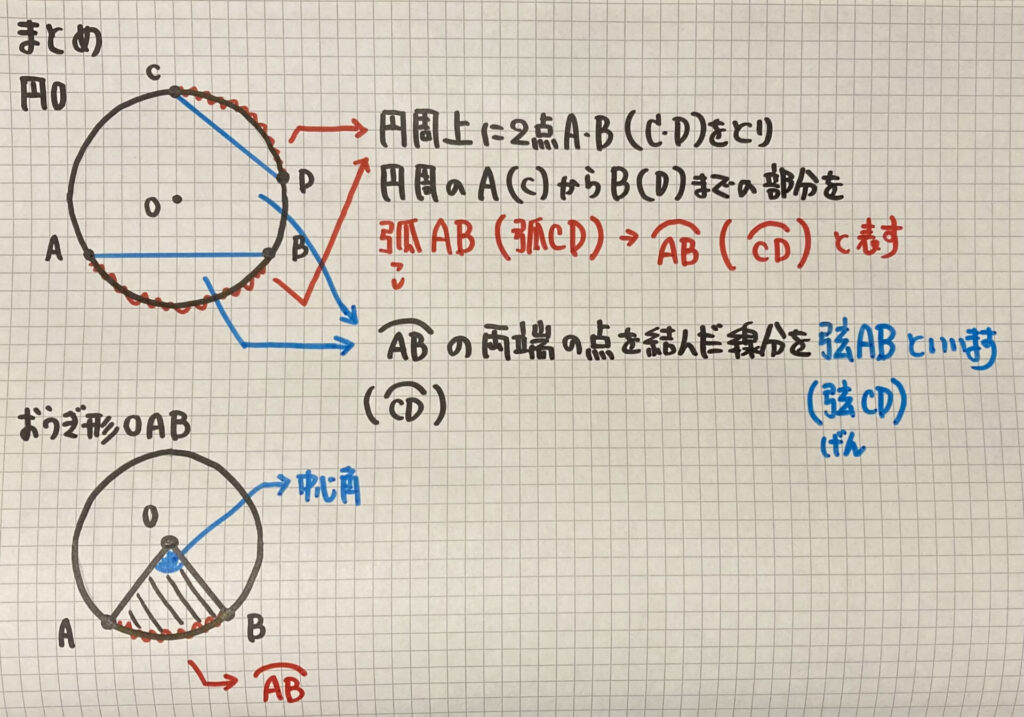
弧(こ)、弦(げん)、中心角について
「算数」で
学習して知っている人も
いるかもしれませんが
まずは言葉の説明です
「読み方」も
確認しておきましょうね
弦、接点、接線について
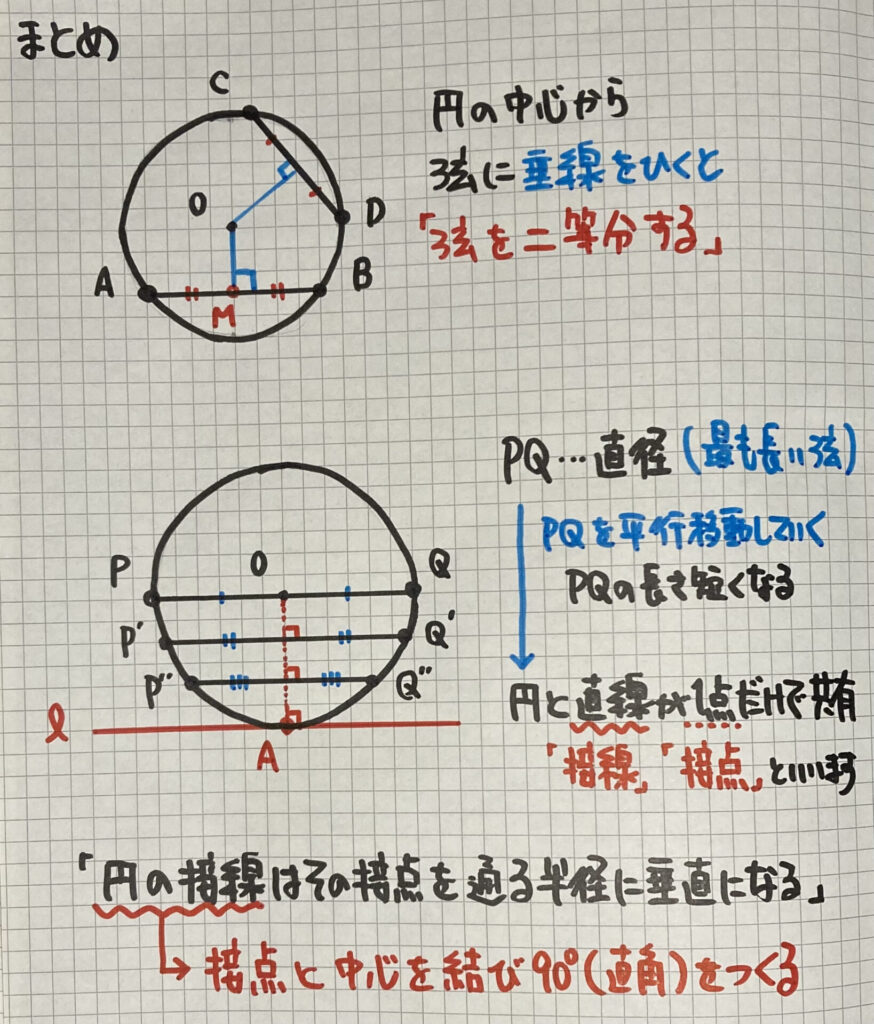
まず言葉の説明です
そして
2つの性質をまとめます
この性質は
大切なのですが
この性質を使って
この2つをできることが
大切になります

実際には
「中3」になってから
使うのですが…
知っておいてくださいね
円と作図
「円と作図」の
よく出てくる問題を
2つご紹介しますね
まずは「接線」です
先ほどまとめた
この性質を使います
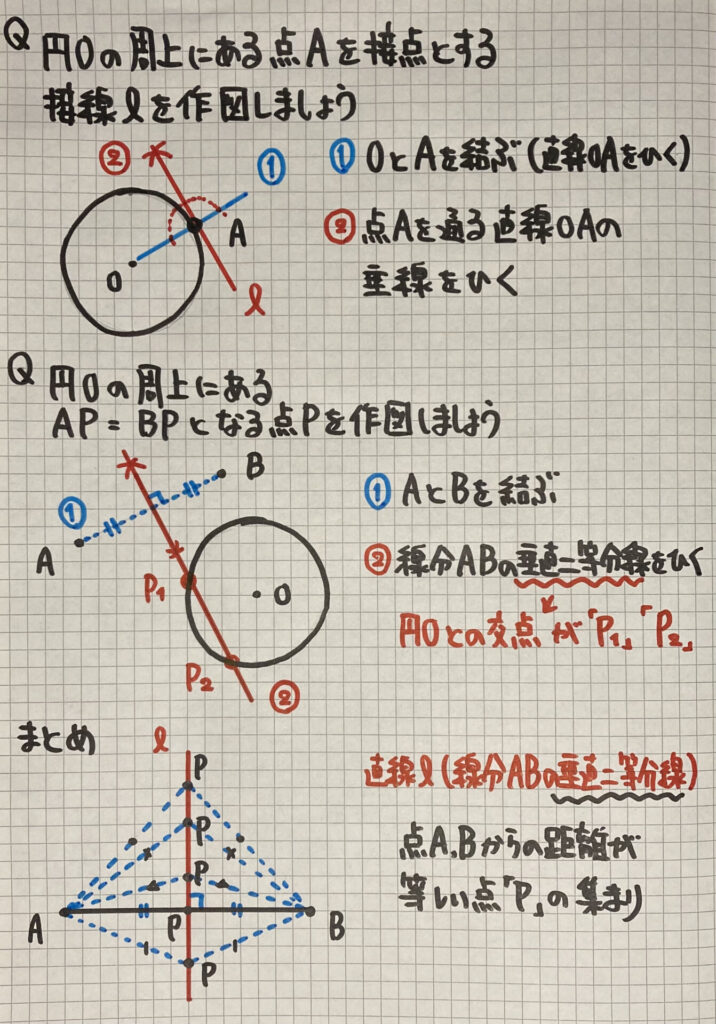
円の接線の作図
- 円の中心と接点を通る直線を引く
- その直線上の接点を通る「垂線の作図」をする
次の作図は
「AP=BPとなる点」
の作図ですが
ということを知っておくと
簡単にできますよ
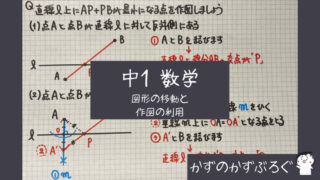
AP=BPとなる点の作図
(2点A,Bから等しい点Pの作図)
(2点A,Bから等しい点Pの作図)
- AとBを結ぶ
- 線分ABの「垂直二等分線の作図」をする
この
「垂直二等分線」と
「距離が等しい点」が
関係する「作図」は
よく出てくるので
知っておいてくださいね
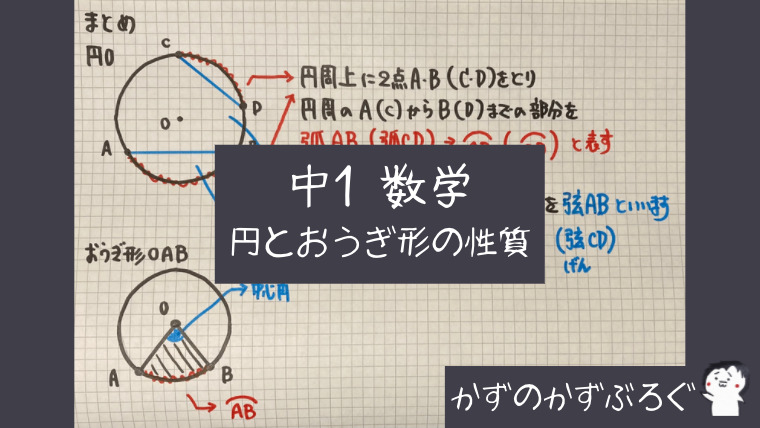
円とおうぎ形の性質のまとめ

・弧(こ)
円周上に2点A、Bをとり
円周のAからBまでの部分
$\stackrel{\huge\frown}{AB}$と表します
・接線、接点
円と直線が
1点だけを共有するとき
「直線は円に【接する】」といいます
その直線のことを「接線」
その点のことを「接点」といいます
・円の中心と弦がある
垂線を引き、弦を二等分します
・接線がある
円の中心と接点を結んで、90°を作ります
・円の接線の作図
- 円の中心と接点を通る直線を引きます
- その直線上の接点を通る「垂線の作図」をします
・AP=BPとなる点の作図
- AとBを結びます
- 線分ABの「垂直二等分線の作図」をします
かずのかず
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした