ここまでで
「数学」の「比例」と「反比例」を
学習してきました
「比例」「反比例」は
こちらで
確認してくださいね
今回はこれらを利用した文章(図形)問題を
一緒に見ていきましょう
「動点」の問題

「数学」でよく出てくる
図形の上を動く点(動点)の問題です
⑴にあるように
三角形の面積は
「底辺×高さ÷2」ではなく
これからは
で表せるようにしておきましょう
「計算が簡単になりますよ」
⑵は「変域」の問題です
BC($x$)の長さは
「0cm以上8cm以下」になるので
「0≦$x$≦8」と表します
面積($y$)の大きさは
最小…$x=0$の時で「0」
最大…$x=8$の時で「24」になるので
「0≦$y$≦24」と表します
⑶は「変域」のあるグラフです
$x(y)$の最小と最大を
- 「以上」「以下」なら「●」
- 「より大きい(小さい)」「未満」なら「○」
にします
最小から最大まで(変域)を
「実線」で書いて
そこ以外を「点線」で書きます
⑷は
比例の式「$y=ax$」に
問題にある$xかy$
(ここでは面積なので$y$ですね)
を代入して求めています
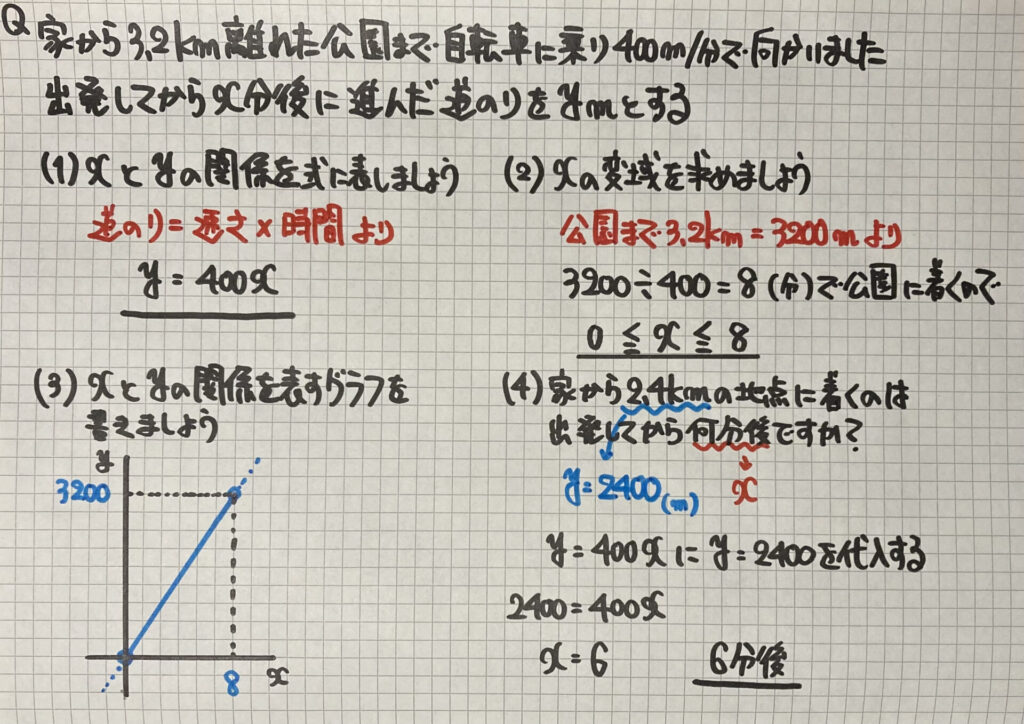
「速さ」の問題
速さの公式何だっけ…?
3つの公式
覚えていなくても
実は大丈夫なんです
「km/時」
この書き方だけ
覚えてください
方程式の文章題で「速さ」の
問題をやりましたね

上の記事で
「速さ」を表すときに
「時速60km」を「60km/時」と
表せることをお伝えしました
この「km/時」に注目してください
例えば、「2分の1」は
「1/2」「$\frac{1}{2}$」で表せますよね
という考え方はできますか?
これがわかりやすければ
もう公式を覚える必要は無くなりますよ

このように
「道のり」や「時間」を求める式を
作ることができます

「自分で作るのは…難しい…」と
思った人は
もちろん、公式を覚えて
使ってくれて大丈夫です
「速さの公式」を
まとめておきますね
ここの問題は
ノートで確認できると
思いますので
しっかり読んでみてください
「歯車」の問題
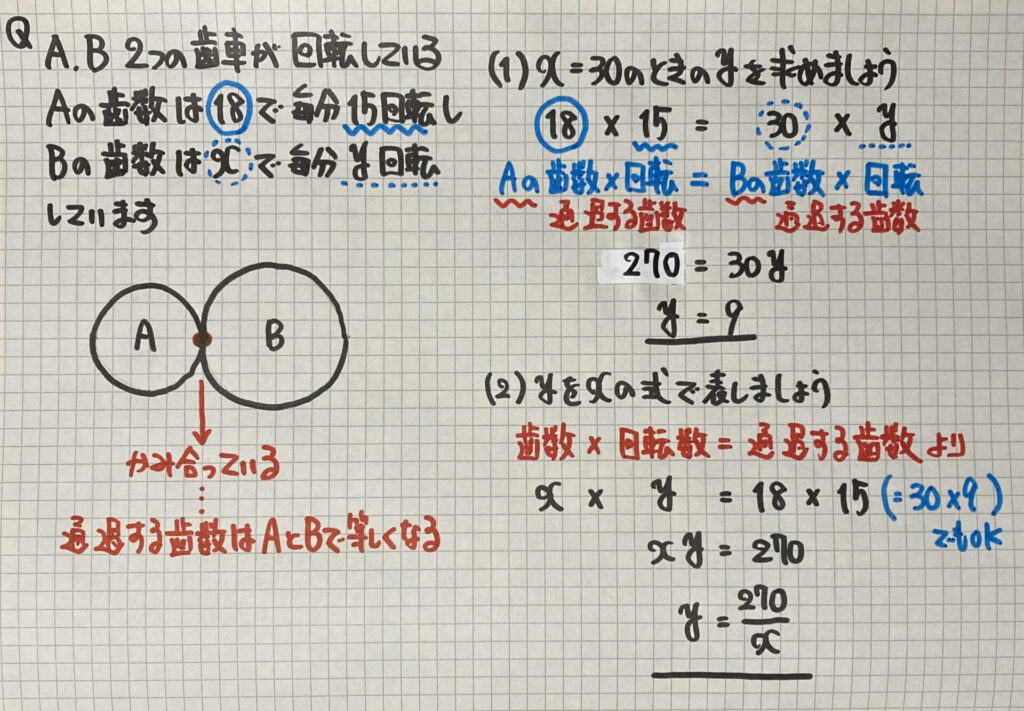
「歯車」の問題は
学校のテストで時々出る
有名な問題です
大切なことは
この式です
「比例?」「反比例?」
どちらでしょうか
「歯数×回転=ある数」になるので
「$x×y=a$」反比例の式になりました
あとは式に代入して求めていきましょう
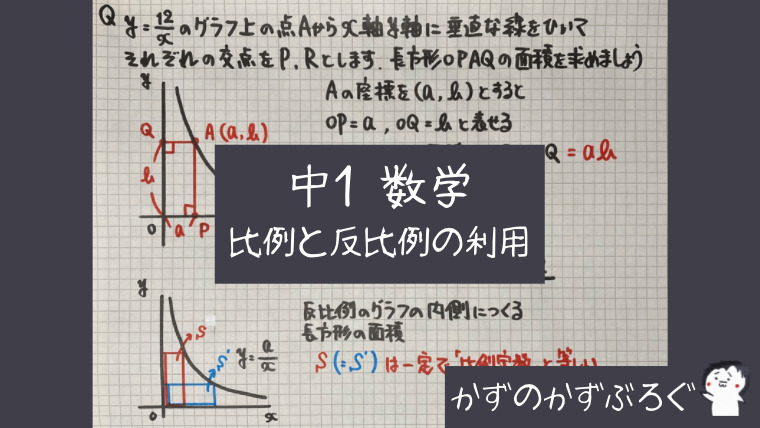
「長方形の面積」の問題
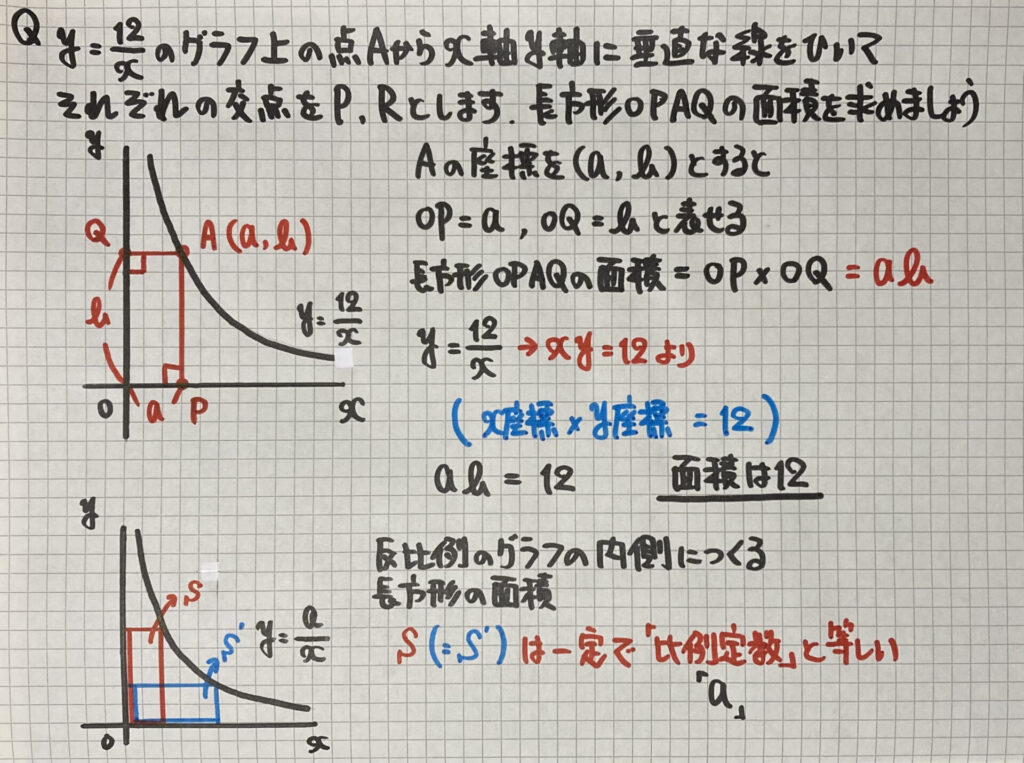
これも有名な問題です
反比例のグラフの
どの点をとっても内側にできる
長方形の面積=たて×横
長方形の面積=「($y$座標)×($x$座標)」
になりますよね
この「($y$座標)×($x$座標)」は
順番を入れかえて書くと
「($x$座標)×($y$座標)=$a$(比例定数)」と
「$a$(比例定数」を求める式になりました
ここまでをまとめると
このことを知っていれば
問題を見ただけで
答えを出すことができますよ
比例と反比例の利用のまとめ

・三角形の面積
$\frac{1}{2}$×底辺×高さ
・変域
$xやy$の
「最小」と「最大」を求める
・速さの公式
速さ(km/時)
=$\frac{km}{時}$
=km÷時(間)
- 速さ=道のり÷時間
- 時間=道のり÷速さ
- 道のり=速さ×時間
・歯車の問題
- Aの歯数×回転=Bの歯数×回転
- 「反比例」の問題
・反比例のグラフの長方形
長方形の面積
=($y$座標)×($x$座標)
=$a$(比例定数)
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした