今回は
「データの活用」の
「ヒストグラムと相対度数」です
「算数」でも
「データの調べ方」を
学習しました

【小6算数】「データの調べ方」の問題 どこよりも簡単な解き方・求め方算数には、いろいろなグラフがありますね「棒グラフ」「折れ線グラフ」「円グラフ」「帯グラフ」「ヒストグラム」(今回見ていきますよ)これらを使って、データ(資料)をまとめたり調べたりすることができます ...
そこでの「言葉」も
出てくるので
忘れてしまっている人は
ここでしっかり
確認してくださいね
最大(小)値 範囲 中央値

まずは
言葉をまとめます
ノートの下の問題で
「中央値」を求める時
データの個数が偶数なら
真ん中「2つの平均」を
求めましょう
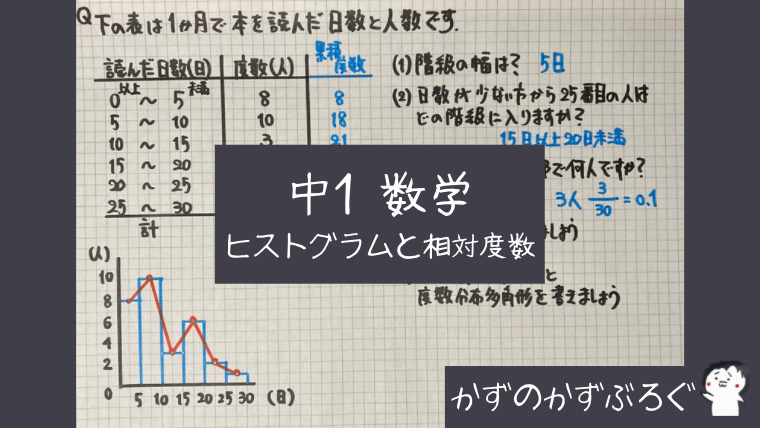
ヒストグラム 度数分布多角形
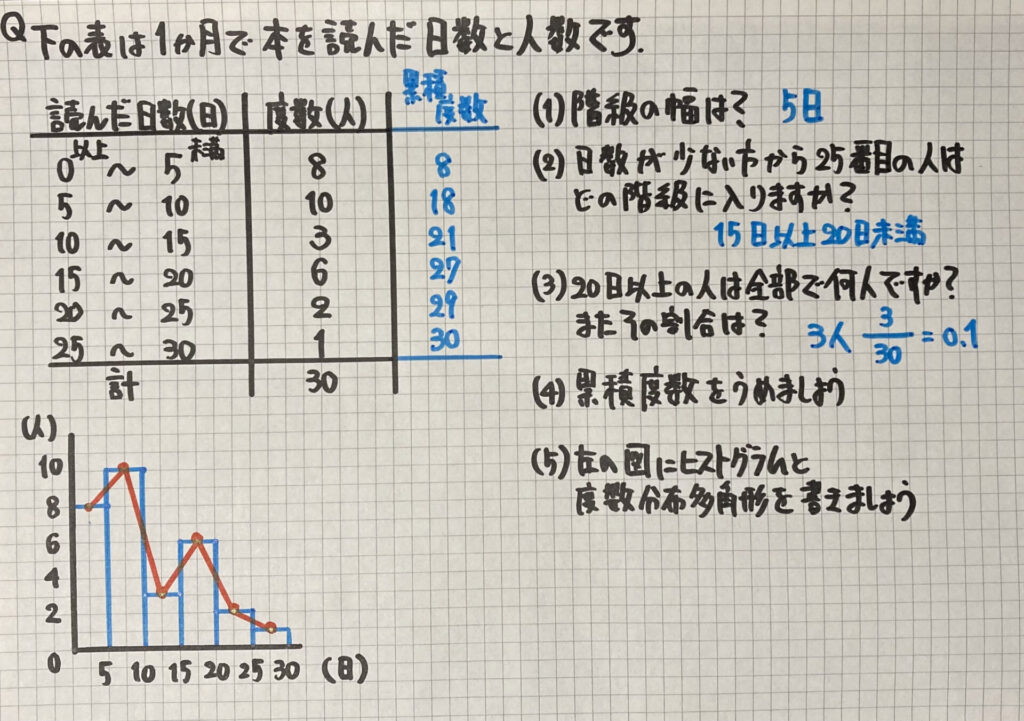
次も
言葉をまとめます
相対度数
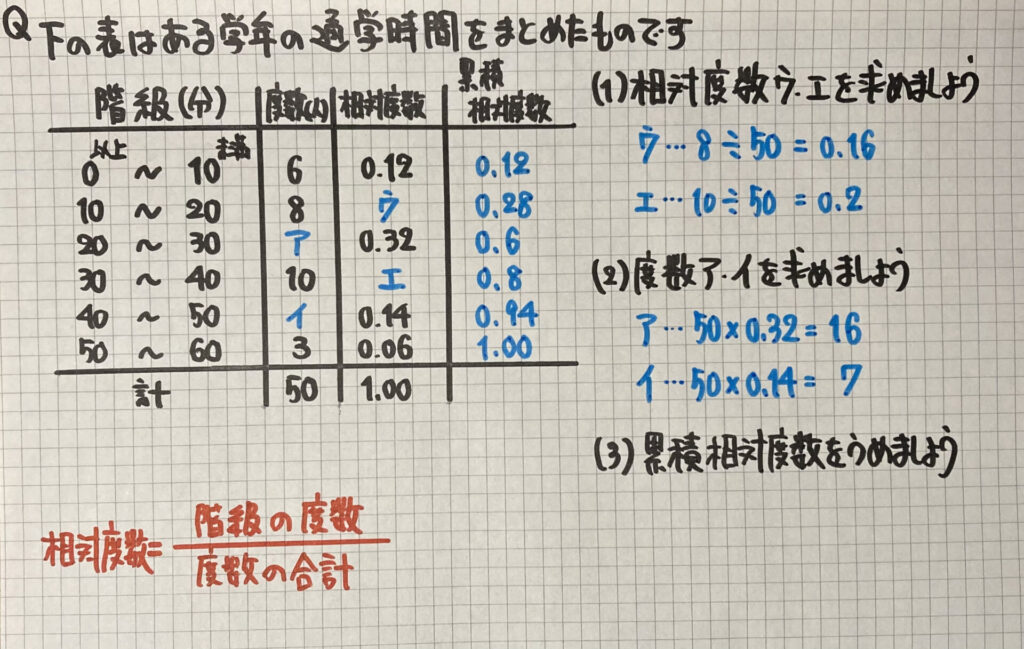
ここでは
「相対度数」や「度数」を
求めて表を完成させます
この式を使って求めましょう
階級値 平均値 最頻値

最後も
言葉をまとめます
ノートにもまとめていますが
平均値の求め方
- (階級値が表にない時は)階級値を求める
- 階級ごとに【階級値×度数】を求める
- $平均値=\frac{階級値×度数の合計}{度数の合計}$で求める
少し計算が大変ですが
求める式は難しくないので
がんばりましょうね
ヒストグラムと相対度数のまとめ

今回は多くの
「言葉」が出てきました
- 最大値(最小値)
- 範囲
- 中央値(メジアン)
- 階級
- 度数
- 度数分布表
- 累積度数
- ヒストグラム(柱状グラフ)
- 度数分布多角形
- 相対度数※
- 累積相対度数
- 階級値
- 最頻値(モード)
- 平均値※
- 「相対度数」を求める式
- 「平均値」を求める式
で分からないものが
あれば、今回の内容を
しっかり見直してくださいね
かずのかず
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした