今回は
「柱体」「錐体」「球」の
体積の求め方を学習します
「柱体」の「体積」については
「算数」でもやりましたね
「角柱と円柱の体積」は
こちらで
確認してください
では、一緒に
見ていきましょう
錐体の体積
次は
「錐体の体積」です
まずは「角錐」です
ノートの立方体を見てください
「3つの合同な四角推」に
分かれていることがわかりますね
ここから
と表すことができます
次は
「円錐」です
ノートの下を見てください
- 「底面の半径」
- 「高さ」が等しい
「円柱」と「円錐」が
あるとします
この「円錐」に
水を満タンに入れて
それを円柱に移すと
全体の$\frac{1}{3}$に
なります
となります
この
×$\frac{1}{3}$
がポイントですね
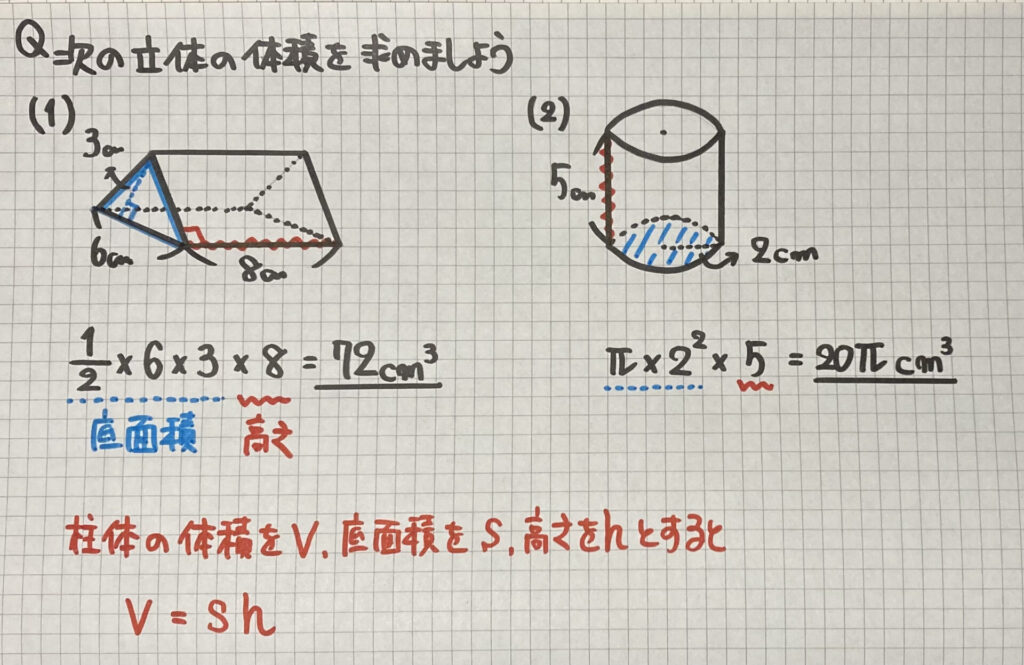
練習問題
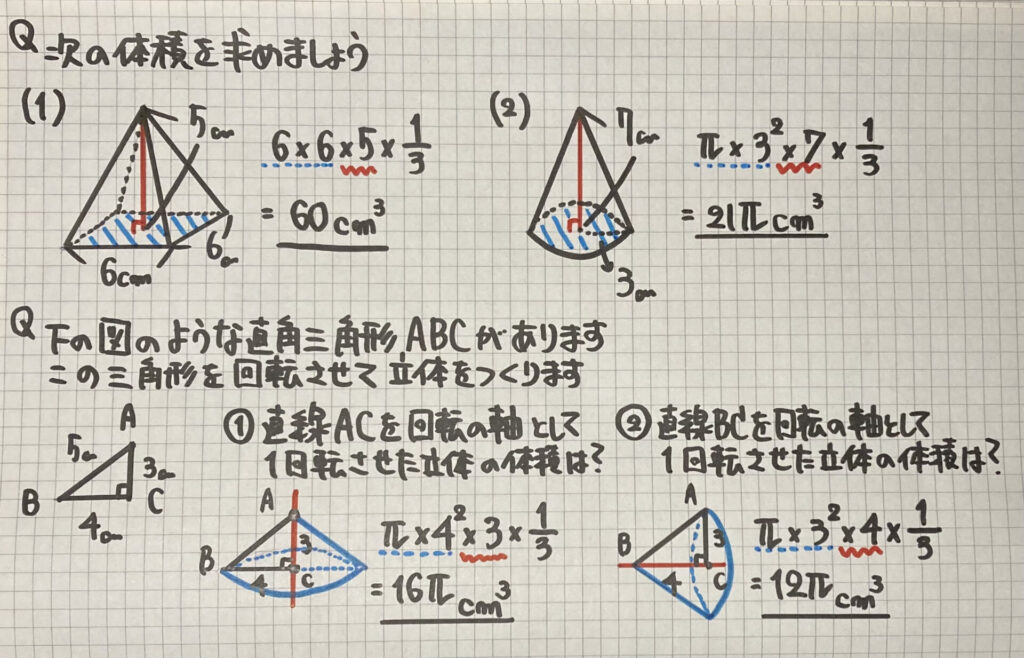
(1)(2)は
×$\frac{1}{3}$を
忘れないように
気をつけましょう
下の問題は
「回転体」ですね
前回学習しましたね
「回転の軸」が
どの「線分」になるのか
間違えないようにしましょう
球の体積
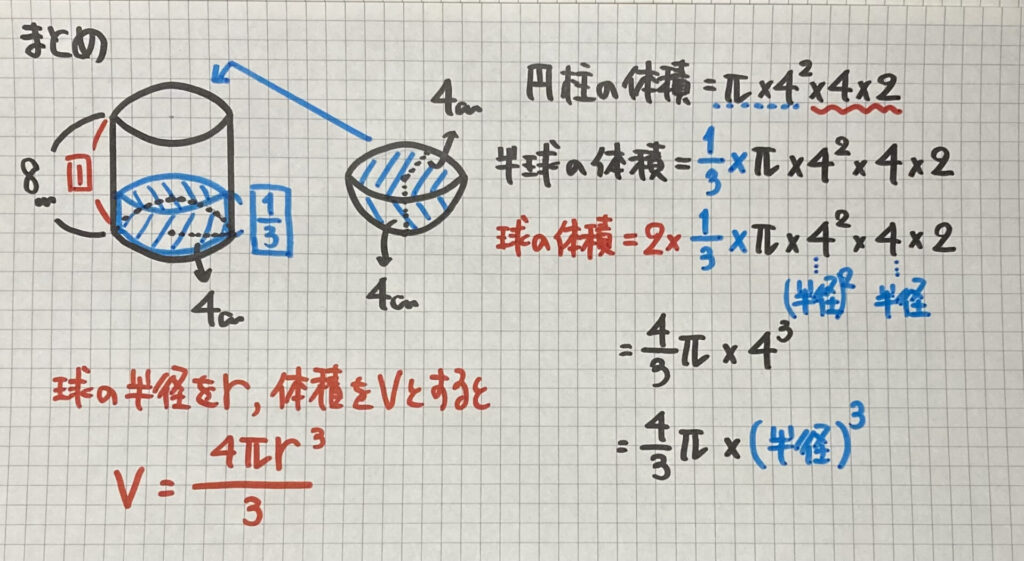
最後に
「球の体積」です
「円錐」の時のように
- 「(底面の)半径」と
- 「高さ(球の直径)」が等しい
「円柱」と「半球」が
あるとします
この「半球」に
水を満タンに入れて
それを円柱に移すと
全体の$\frac{1}{3}$に
なります
ノートの右の式を
見てください
半球の体積=$\frac{1}{3}$×円柱の体積なので
球の体積=$\frac{2}{3}$×円柱の体積
となりますが
この式だと
「球の体積」を求める時に
毎回、円柱を考えないと
いけないので大変です
そこで
円柱の体積を求める式を
見てください
円柱の高さの8cmを
「4cm×2」と
「球の半径×2」のように
考えます
すると
ノートにあるように
(半径)が「3つ」出てきます
そこで
自分で覚えやすい方で
しっかり覚えましょうね
練習問題

立体の
上の部分を「円錐」
下の部分を「半球」に
分けて、それぞれ
計算して求めましょう
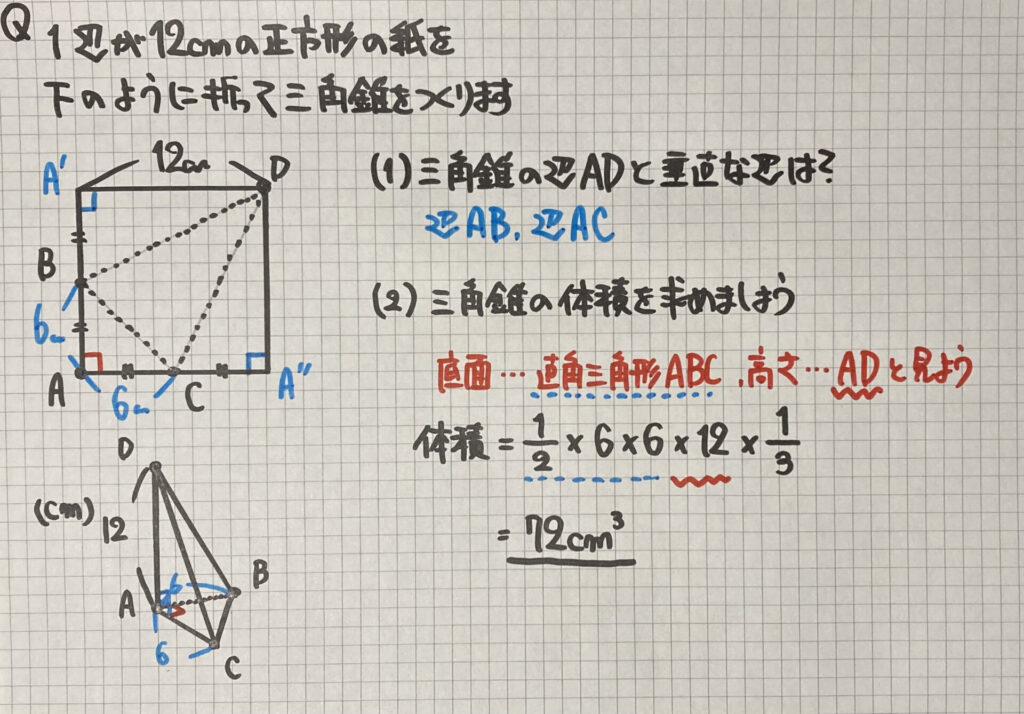
学校のテストに
よく出る問題です
ポイントは
正方形の頂点
- 左上のA’と
- 右下のA”が
- 左下のAと
重なることです
一度学習すると
「三角錐」の形が
分かると思います
是非、自分でも
「三角錐」を
書いてみてください
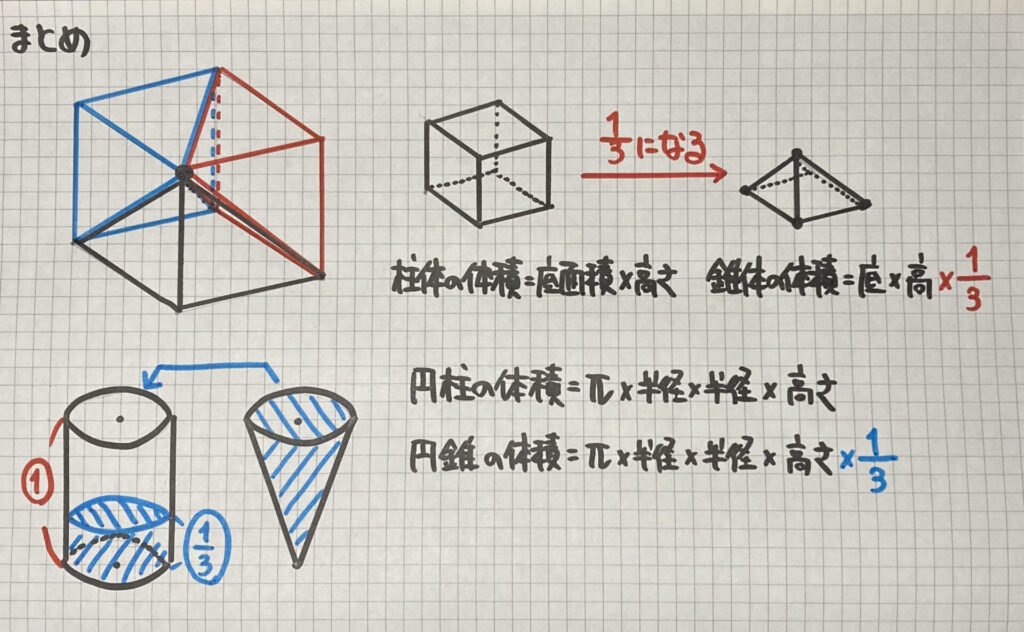
立体の体積のまとめ

・柱体の体積
柱体の体積をV 底面積をS 高さをhとすると
V=Sh
・角推の体積
角錐の体積をV 底面積をS 高さをhとすると
V=$\frac{1}{3}$Sh
・円錐の体積
円錐の体積をV 底面の半径をr 高さをhとすると
$\frac{1}{3}$$π$×$r^2$×h
・球の体積
球の半径をr 体積をVとすると
V=$\frac{4πr^3}{3}$
文字で覚えにくい人は
「底面積」や「高さ」「半径」を
使って覚えても大丈夫です!
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした