前回までに
「展開(乗法公式)」
「因数分解」と
計算について
学習してきました
こちらで
確認してくださいね
これらを利用して
いろいろな問題を
簡単に解く方法を
一緒にやっていきましょう
展開・因数分解の利用
まずは
計算の問題です
筆算を使えば
どの問題も
答えを出すことはできます
もし、問題文に
「工夫して」
「展開(因数分解)を利用して」
等が書いてあれば
ノートのような
「途中の式」が
必要になります
最初は
「問題を見て、すぐに思いつかない…」
と思う人がいると思います
これらの計算は
練習をすることで
気づけるようになるので
式の値
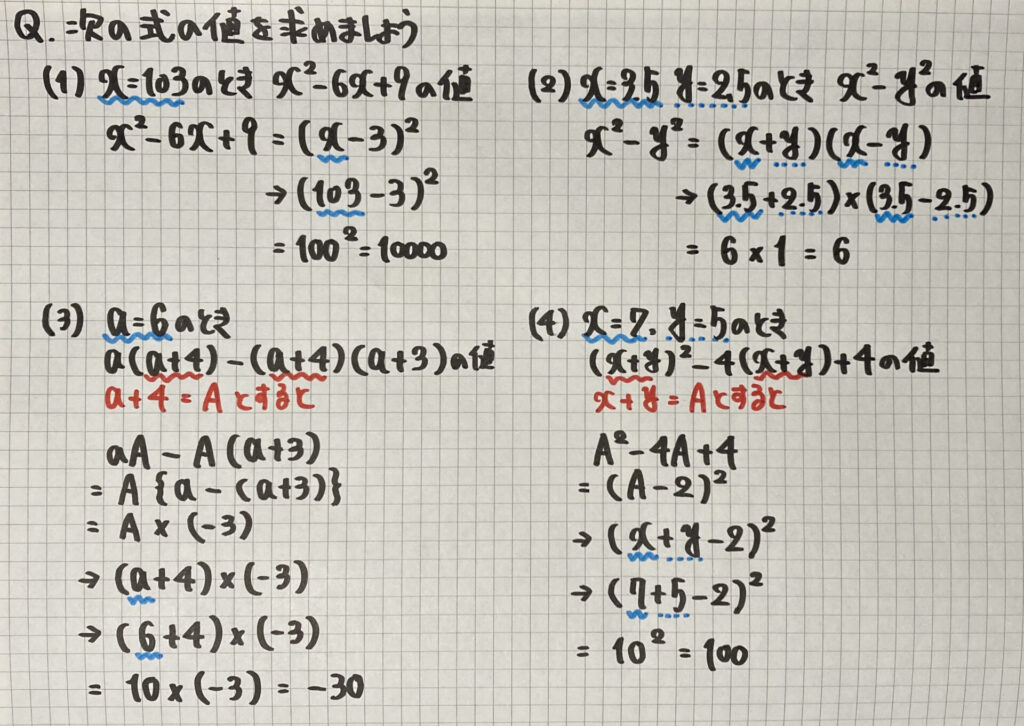
「中1」「中2」でも
学習した「式の値」です
ここでは
を使って解いていきましょう
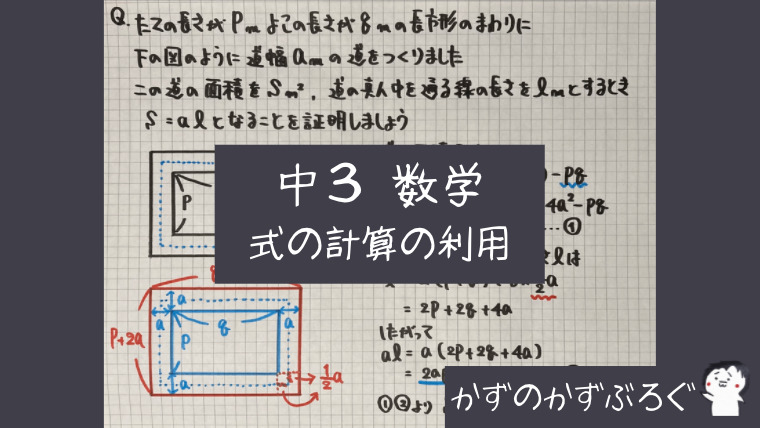
道の面積
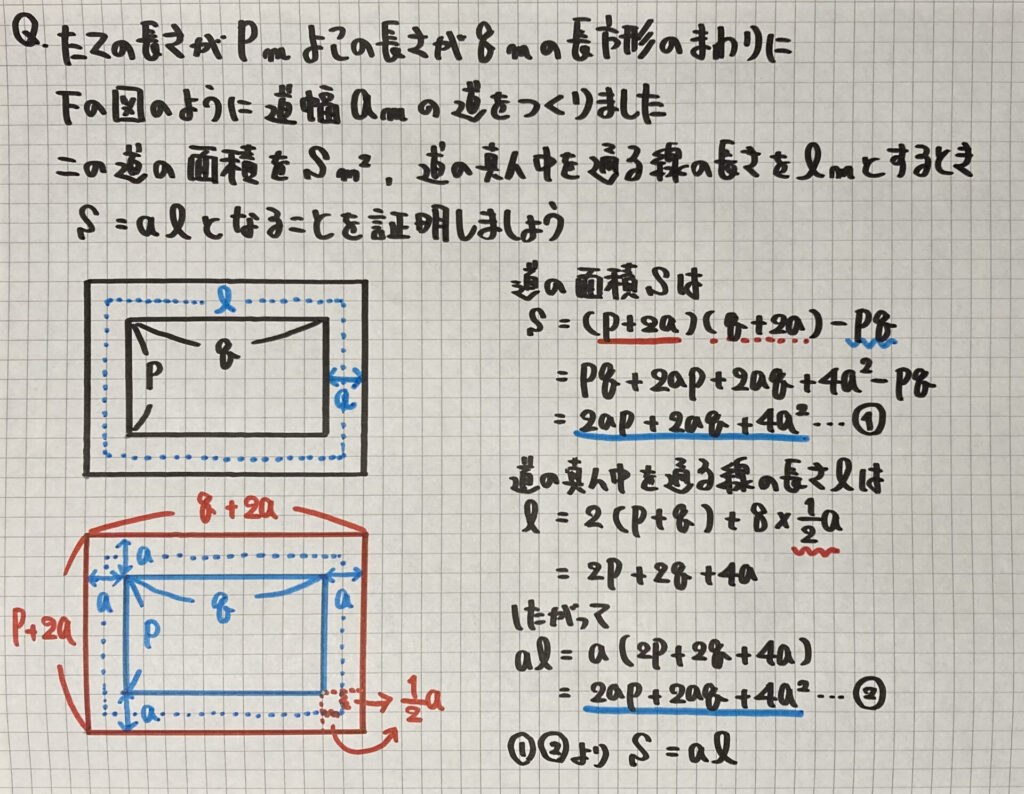
教科書や問題集
学校のテスト
によく出てくる
有名な問題です
道の面積(S)は
「大きい長方形ー小さい長方形」
$(p +2a)(q +2a)-pq$で
求めることができます
道を通る線(ℓ)は
「小さい長方形の周りの長さ＋四角の長さ」
$2(p +q)+8×\frac{1}{2}a$で
求めることができます
あとは
ノートにある流れで
書いていきましょう
詳しくは
「高校数学」で
学習しますが
整数の証明
中2で
「式の説明」や「証明」を
学習しました
内容はその時と同じです
【中2数学】「式の説明と等式変形」の問題 どこよりも簡単な解き方・求め方前回まで学習してきた「単項式・多項式の計算」を使って「式の説明」と「等式変形」を学習していきます...
書き方は
いろいろあるので
学校のテストでは
習った形で書くようにしましょう
こちらが、大きな流れです
式の証明の書き方
- 「（文字）を整数とすると、…は（文字式）で表せる」
- 問題文にある計算をする
- 「（文字）は整数より（文字式）も整数なので（文字式）は…である」
- 「したがって（問題文の結論）」でまとめる
式の計算の利用のまとめ
・展開・因数分解の利用
問題文に
「工夫して」
「展開(因数分解)を利用して」とある時
公式を利用して簡単に計算する
・式の値
- 「乗法公式」
- 「因数分解」の公式
- 「置き換え」の利用
を使って解いていく
・道の面積
道の面積(S)＝道幅($a$)×道のり(道を通る直線ℓ)
・整数の証明の書き方
- 「（文字）を整数とすると、…は（文字式）で表せる」
- 問題文にある計算をする
- 「（文字）は整数より（文字式）も整数なので（文字式）は…である」
- 「したがって（問題文の結論）」でまとめる
以上、「数学嫌いな人が、
数学を楽しく好きになって欲しい」
かずのかずぶろぐでした
